Proof: f(x) = |x| is Continuous using Epsilon Delta Definition | Real Analysis Exercises

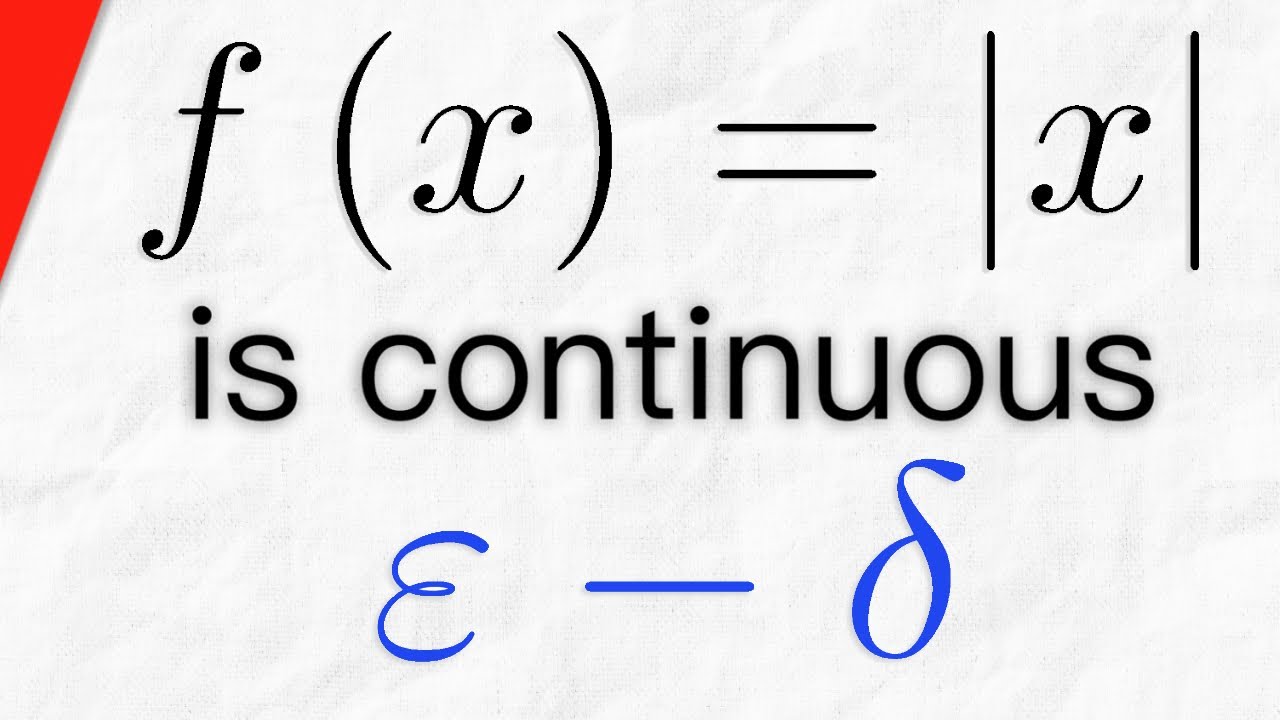
Показать описание

We prove that f(x)=|x|, also known as f(x)=abs(x), the absolute value function, is continuous on the real numbers. We complete this proof using the epsilon delta definition of continuity of a function at a point. To do this, we simply take an epsilon greater than 0 and an arbitrary point c from our domain, then go through the motions of finding a delta greater than 0 so that any x in R that is within delta of c has an image within epsilon of c's image. We'll need the reverse triangle inequality theorem and not much else! Let me know if there are more epsilon delta continuity proofs you want to see!

#Math #RealAnalysis

★DONATE★

Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!

Follow Wrath of Math on...

Рекомендации по теме

Комментарии

every week in my calc 1 class I find myself coming back to this channel, I cant thank you enough haha

MajesticQT

Reverse triangle inequality!
Brilliant! 😁

punditgi

If you find these videos helpful, please share them with others who may find them useful too! It's a big help!

WrathofMath

This is the only video that made me understand on how to work with these problems ..thank you!

life_with_aida

Proof: f(x) = |x| is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Proof: f(x) = |x| is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Proof: f(x) = x is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Proof that f(x) = 1/x is Continuous on (0, infinity) using Delta-Epsilon

Proof that f(x) = x*|x| is Differentiable at x = 0

Proof formula Integral f(x)dx from 0 to a

Proof that f(x) = x^2 is Uniformly Continuous on (0, 1)

Proof f(x)=sin(x) is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Proof that f(x) = 1/x is not Uniformly Continuous on (0,1)

FORZA 5 FERRARI FXX-K EVO #fyp #foryou #forza #forzahorizon5go #drift #viral

Prove f(x) = x^3 is a bijection. Set Theory. Abstract Algebra

Show that f(x) is continuous at x=4

Prove the function f:Z x Z → Z given by f(m,n) = 2m - n is Onto(Surjective)

Injective Functions | Is f(x)=x^2 Injective? | A formal proof | Analysis | Math2Go

Power Rule of Derivative Calculus - Proof f ' (X to the power n) = n.X to the power (n-1)

Prove that if f(x) = log(x/(x - 1)) then f(y + 1) + f(y) = log((y + 1)/(y - 1))

Determine if f(x) = x + 1/x is an Even or Odd Function

Derivatives - Proof why f'(a^x) = ln(a)a^x

How to Prove the Rational Function f(x) = 1/(x - 2) is Surjective(Onto) using the Definition

Proving the Function f(x) = sqrt(x + 2) is One to One(Injective) using the Definition

Proving a Function is a Linear Transformation F(x,y) = (2x + y, x - y)

Prove that the function `f(x)=x^n`is continuous at `x = n`, where n is a positive integer.

Prove that the identity function on real numbers given by `f(x) = x` is continuous at every real...

Prove f(x + a) - f(x - a) = 2a/(a^2 - x^2) if f(x) = 1/x

#07 prove that f(x)=1/x^2 is uniform contiouous on [a ,infinite) but not UC on (0, infinite)