Proof: e^x is Continuous using Epsilon Delta Definition | Real Analysis Exercises

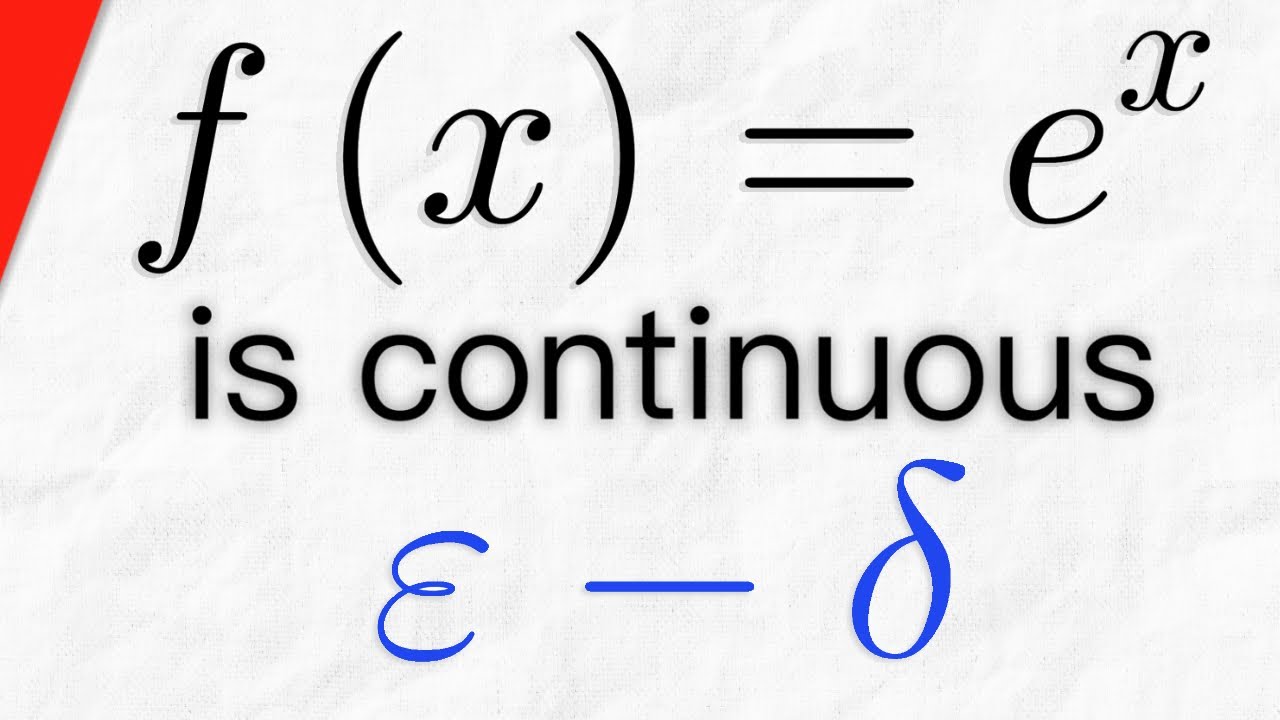
Показать описание

We prove that f(x)=e^x, the natural exponential function, is continuous on its entire domain - the real numbers. We complete this proof using the epsilon delta definition of continuity of a function at a point. To do this, we simply take an epsilon greater than 0 and an arbitrary point c from our domain, then go through the motions of finding a delta greater than 0 so that any x in D that is within delta of c has an image within epsilon of c's image. However, we'll quickly find that our problem gets reduced to proving e^x is continuous at 0. Also, we will be using the power series definition of e^x for this proof. Let me know if there are more epsilon delta continuity proofs you want to see!

#RealAnalysis #Math

★DONATE★

Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!

Follow Wrath of Math on...

Рекомендации по теме

Комментарии

Questions:

1) As a general rule, is it logically sound to do Taylor series to find a relationship between delta and epsilon? My concern is if the Taylor series somehow assumes the existence of a limit -- in which case our proof is circular -- but I guess that's not actually a problem, right?

2) Being very formal, delta needs to be the minimum of 1 and epsilon / (epsilon + 1), right?

3) In most of the examples I've seen, the relationship between delta and epsilon is linear; it's not in this case. Do I take it that really all that's required is, as delta goes to zero, so does epsilon?

kingbeauregard

Can you make a playlist on polynomials in depth

krasimirronkov

how about e^(-x)? are the steps still the same, just that we change the x into -x ?

Kane

If you are using the power series representation for e^x, you are assuming e^x is analytic, which implies that e^x is continuous, which is circular logic

awvz_

so do we not need to fill in that first delta?

odobenusrosmarus

Proof: e^x is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Proof: e^x is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Proof: f(x) = |x| is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Proof: f(x) = x is Continuous using Epsilon Delta Definition | Real Analysis Exercises

proving x^2 is continuous using the epsilon delta definition

Proof: ax+b is Continuous using Epsilon Delta Definition

Proof f(x)=sin(x) is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Prove that exponential function is a continuous function | In English

Proof: sqrt(x) is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Lecture 4(PDEs): Fourier Theorem

Proof that f(x) = 1/x is Continuous on (0, infinity) using Delta-Epsilon

Real Analysis Proofs - Exponential Function is Continuous

3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus

Differentiable then Continuous Proof

Show that f(x) is continuous at x=4

Proving x^2 is continuous (with epsilon delta definition)

How to prove a function is not continuous using limit definition of continuity | Math with Janine

Determine if the Piecewise Function is Continuous by using the Definition of Continuity

e to the power x is a Continuous function

Proof of a Limit Value Using Epsilon and Delta

Polynomials and Rational Functions are Continuous | Real Analysis

How to determine if a function is continuous and differentiable

What is the number 'e' and where does it come from?

What's so special about Euler's number e? | Chapter 5, Essence of calculus

Prove the Piecewise Function is Continuous with the Delta-Epsilon Definition of Continuity