filmov
tv
Proof: A Useful Absolute Value Inequality | Real Analysis

Показать описание
For real numbers a and b, |a| is less than or equal to b if and only if -b is less than or equal to a is less than or equal to b. We'll prove this useful theorem about the absolute value in today's real analysis lesson!
This theorem gives us a way to go from an absolute value inequality (|a| is less than or equal to b) to a nice inequality with no absolute value! We can of course also use the other direction of the theorem in order to PROVE an absolute value relationship. If we want to prove that |a| is less than or equal to b, we just need to show that -b is less than or equal to a is less than or equal to b. That is the power of this result, it helps us work with absolute value! The basic idea is that if |a| is less than or equal to b, it must be the case that -b is more negative than a and b is more positive than a. Thus, whether a is positive or negative, its magnitude is less than b. Notice if b is greater than or equal to |a|, then b must be non-negative.
I hope you find this video helpful, and be sure to ask any questions down in the comments!
********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.
********************************************************************
+WRATH OF MATH+
Follow Wrath of Math on...
This theorem gives us a way to go from an absolute value inequality (|a| is less than or equal to b) to a nice inequality with no absolute value! We can of course also use the other direction of the theorem in order to PROVE an absolute value relationship. If we want to prove that |a| is less than or equal to b, we just need to show that -b is less than or equal to a is less than or equal to b. That is the power of this result, it helps us work with absolute value! The basic idea is that if |a| is less than or equal to b, it must be the case that -b is more negative than a and b is more positive than a. Thus, whether a is positive or negative, its magnitude is less than b. Notice if b is greater than or equal to |a|, then b must be non-negative.
I hope you find this video helpful, and be sure to ask any questions down in the comments!
********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.
********************************************************************
+WRATH OF MATH+
Follow Wrath of Math on...
Комментарии
 0:07:45
0:07:45
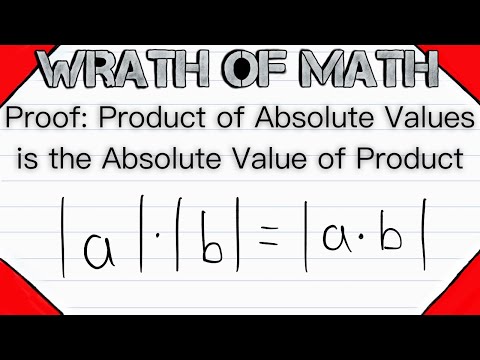 0:05:15
0:05:15
 0:04:21
0:04:21
 0:06:43
0:06:43
 0:03:37
0:03:37
 0:07:42
0:07:42
 0:09:49
0:09:49
 0:09:42
0:09:42
 0:45:33
0:45:33
 0:06:03
0:06:03
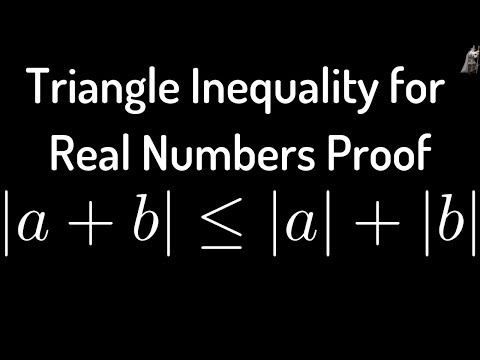 0:03:08
0:03:08
 0:06:47
0:06:47
 0:00:49
0:00:49
 0:09:49
0:09:49
 0:00:50
0:00:50
 0:03:31
0:03:31
 0:03:24
0:03:24
 0:05:31
0:05:31
 0:05:45
0:05:45
 0:13:56
0:13:56
 0:08:35
0:08:35
 0:08:53
0:08:53
 0:05:30
0:05:30
 0:00:24
0:00:24