filmov
tv
Solving First order linear differential equation

Показать описание
In this video, I showed how to use an integrating factor to solve a 1st order differential equation. Thanks to those who observed the mistake in the earlier version of this video. Your help is immensely appreciated.
First Order Linear Differential Equations
First Order Linear Differential Equation & Integrating Factor (introduction & example)
Solving First order linear differential equation
How to Solve First Order Linear Differential Equations
Solving First-Order Linear Differential Equations - Introduction with Examples
The Method of Integrating Factors for Linear 1st Order ODEs **full example**
Solving Linear Differential Equations with an Integrating Factor (Differential Equations 16)
Linear Differential Equations & the Method of Integrating Factors
how to approximate like a physicist | Euler's Method & Runge-Kutta #somepi
How to use the Integrating Factor Method (First Order Linear ODE)
Systems of linear first-order odes | Lecture 39 | Differential Equations for Engineers
Introduction to Linear Differential Equations and Integrating Factors (Differential Equations 15)
Solving a First Order Linear Differential Equation
🔵15 - Linear Differential Equations: Initial Value Problems (Solving Linear First Order ODE's)...
first order linear differential equation, 2.3#19
🔵24 - D Operator Method for Solving First Order Linear Differential Equations
Finding particular linear solution to differential equation | Khan Academy
Solving a first order linear diff eq (integrating factor, method of undetermined coefficient)
First Order Linear Differential Equations / Integrating Factors - Ex 2
First order, Ordinary Differential Equations.
Solving Linear First-Order Differential Equations: Integrating Factor Method
Differential equation introduction | First order differential equations | Khan Academy
Solving First Order Linear Differential Equations 3 Examples
Euler's Method Example (first order linear differential equation)
Комментарии
 0:22:28
0:22:28
 0:20:34
0:20:34
 0:11:52
0:11:52
 0:10:53
0:10:53
 0:09:26
0:09:26
 0:05:07
0:05:07
 1:11:01
1:11:01
 0:11:36
0:11:36
 0:13:32
0:13:32
 0:03:44
0:03:44
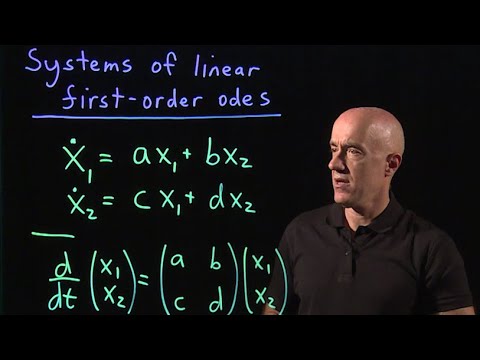 0:08:28
0:08:28
 1:07:16
1:07:16
 0:02:50
0:02:50
 0:21:16
0:21:16
 0:10:44
0:10:44
 0:39:06
0:39:06
 0:06:30
0:06:30
 0:18:43
0:18:43
 0:03:30
0:03:30
 0:48:35
0:48:35
 0:11:48
0:11:48
 0:07:49
0:07:49
 0:29:28
0:29:28
 0:06:18
0:06:18