filmov
tv
Solving a first order linear diff eq (integrating factor, method of undetermined coefficient)

Показать описание
0:00 use integrating factor
6:47 undetermined coefficient
6:47 undetermined coefficient
First Order Linear Differential Equations
How to Solve First Order Linear Differential Equations
First Order Linear Differential Equation & Integrating Factor (introduction & example)
Solving First-Order Linear Differential Equations - Introduction with Examples
Learning First Order Linear DE in 30 Minutes!
The Method of Integrating Factors for Linear 1st Order ODEs **full example**
Introduction to Linear Differential Equations and Integrating Factors (Differential Equations 15)
Solving Linear Differential Equations with an Integrating Factor (Differential Equations 16)
Substitution Suggested by Differential Equations Part 2 (Live Stream)
Solving a First Order Linear Differential Equation
Solving a first order linear diff eq (integrating factor, method of undetermined coefficient)
Linear Differential Equations & the Method of Integrating Factors
Systems of linear first-order odes | Lecture 39 | Differential Equations for Engineers
First order linear difference equations
How to use the Integrating Factor Method (First Order Linear ODE)
Finding particular linear solution to differential equation | Khan Academy
🔵15 - Linear Differential Equations: Initial Value Problems (Solving Linear First Order ODE's)...
First order, Ordinary Differential Equations.
First-Order Linear Differential Equations & Integrating Factors (Introduction)
first order linear differential equation, 2.3#19
Separable First Order Differential Equations - Basic Introduction
systems of first order linear equations -- differential equations 21
Calculus 2 Lecture 8.1: Solving First Order Differential Equations By Separation of Variables
Discrete Math II - 8.2.1 Solving First-Order Linear Homogeneous Recurrence Relations
Комментарии
 0:22:28
0:22:28
 0:10:53
0:10:53
 0:20:34
0:20:34
 0:09:26
0:09:26
 0:42:08
0:42:08
 0:05:07
0:05:07
 1:07:16
1:07:16
 1:11:01
1:11:01
 1:08:41
1:08:41
 0:02:50
0:02:50
 0:18:43
0:18:43
 0:11:36
0:11:36
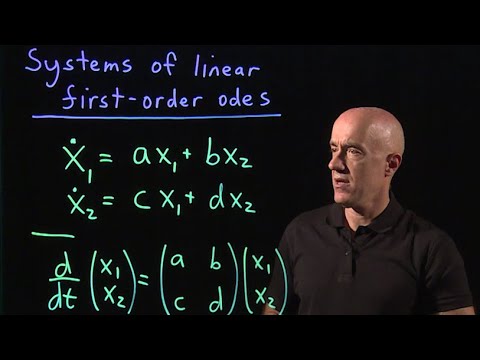 0:08:28
0:08:28
 0:07:25
0:07:25
 0:03:44
0:03:44
 0:06:30
0:06:30
 0:21:16
0:21:16
 0:48:35
0:48:35
 0:12:05
0:12:05
 0:10:44
0:10:44
 0:10:42
0:10:42
 0:34:02
0:34:02
 2:49:22
2:49:22
 0:14:31
0:14:31