filmov
tv
Solving a Golden Radical Equation

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#Algebra #radicals #GoldenRatio
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#Algebra #radicals #GoldenRatio
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving a Golden Radical Equation
Solving a Golden Radical Equation
A Wonderful Math Problem. Olympiad Radical Equation Solving. The Golden Ratio.
A Golden Radical Equation
How to Solve a Radical Equation with Golden Flavor
A Golden Radical Equation
Simplifying a Golden Radical Expression in Three Ways
A Radical Equation with Golden Flavor
A Radical Equation with Golden Flavor. Radical equations part 1
A Golden Radical and Powers of Golden Ratio
Learn Two Methods to Solve the Radical Equation | Math Olympiad Training
Solving A Radical Equation in Three Ways
#9. Solve the Radical Equation with Two Square Roots
Solving a radical equation
Can You Solve these If-Then Radical Equations? | Step-by-Step Explanation
PreCalculus | Solving a Radical Equation
An Infinite Radical Equation
Solving An Interesting Radical Equation | Maths and Science Channel |
Simplify Radical Expressions (Quadratic Equation Form)
Canadian Math Olympiad - Interesting Radical Equation in Golden Ratio
A Radical Equation with a Radical Solution
Solving a radical equation. Algebra challenge.
Solving a Radical Equation with Unlike Roots
Solving A Homemade Infinite Radical Equation
Комментарии
 0:13:50
0:13:50
 0:13:50
0:13:50
 0:08:01
0:08:01
 0:00:33
0:00:33
 0:12:26
0:12:26
 0:05:34
0:05:34
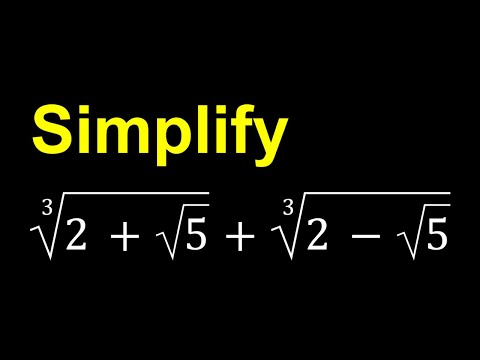 0:10:55
0:10:55
 0:12:26
0:12:26
 0:12:16
0:12:16
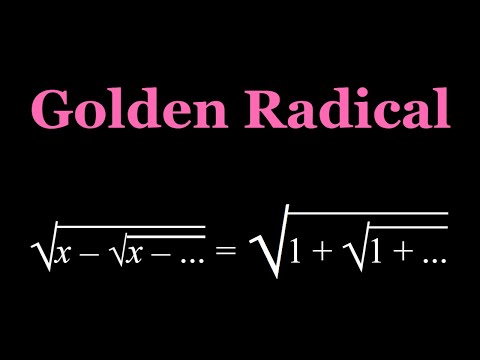 0:09:06
0:09:06
 0:09:41
0:09:41
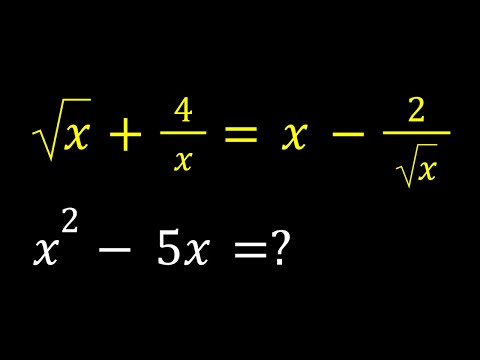 0:08:59
0:08:59
 0:05:17
0:05:17
 0:08:08
0:08:08
 0:10:14
0:10:14
 0:03:36
0:03:36
 0:04:29
0:04:29
 0:11:09
0:11:09
 0:06:10
0:06:10
 0:07:51
0:07:51
 0:05:09
0:05:09
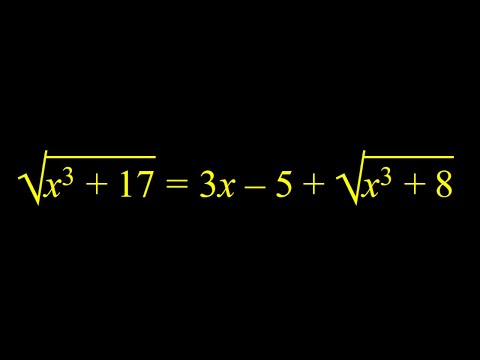 0:10:09
0:10:09
 0:07:05
0:07:05
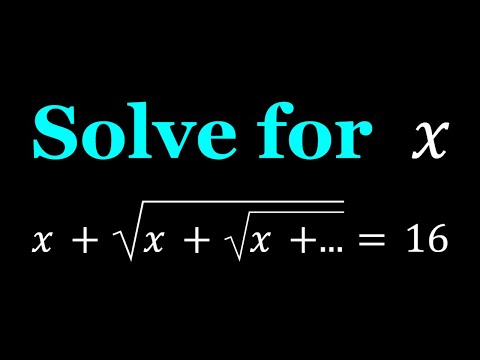 0:09:21
0:09:21