filmov
tv
A Golden Radical and Powers of Golden Ratio

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #SequencesAndSeries
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #SequencesAndSeries
EXPLORE 😎:
PLAYLISTS 🎵 :
A Golden Radical and Powers of Golden Ratio
A Golden Radical Equation
A Wonderful Math Problem. Olympiad Radical Equation Solving. The Golden Ratio.
An Infinite Radical Expression | The Golden Ratio
Solving a Golden Radical Equation
How to Solve a Radical Equation with Golden Flavor
Germany Math Olympiad Problem #shorts #maths #mathematics #radical #olympiad #algebra
A Nice Math Olympiad Problem #shorts #maths #mathematics #radical #olympiad #algebra
Cole Williams - [Radical Healing Session LIVESTREAM]
Solving a Golden Radical Equation
Olympiad Question: Solve this radical rational Equation | Fast & Easy Method!
Math Olympiad Question | How to Simplify Radical Problem | Math Olympiad Training
A Nice Math Olympiad Exponential Problem #shorts #maths #mathematics #radical #olympiad #algebra
A Radical Equation with Golden Flavor
A Golden Radical Equation
Can you solve this Radical Expression in 30 Seconds? | Fast & Easy Trick
Norway Math Olympiad Problem #shorts #maths #mathematics #radical #olympiad #algebra
Solving a Radical Equation with a Cube Root and Higher Powers (Example)
Orthodox Christian Priest against radical islamist militias ☦️☦️☦️
A Radical Exponential Equation #maths
How Are Radicals Used in Everyday Life? : Radical Numbers
Surds (Radicals): Golden Rules when raising a SURD (radical) to a power
Calculators NOT Allowed! | Simplify this Radical if You're a GENIUS! |
China Math Olympiad Problem #shorts #maths #mathematics #radical #olympiad #algebra
Комментарии
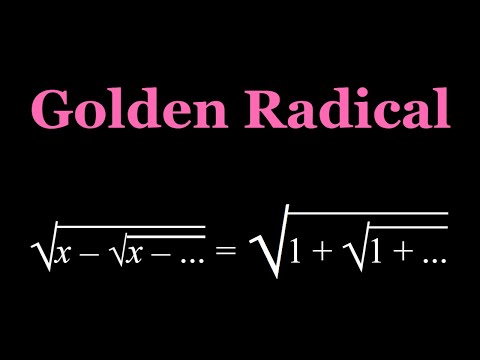 0:09:06
0:09:06
 0:00:33
0:00:33
 0:08:01
0:08:01
 0:09:33
0:09:33
 0:13:50
0:13:50
 0:12:26
0:12:26
 0:00:06
0:00:06
 0:00:05
0:00:05
 1:28:06
1:28:06
 0:13:50
0:13:50
 0:05:40
0:05:40
 0:06:42
0:06:42
 0:00:05
0:00:05
 0:12:26
0:12:26
 0:05:34
0:05:34
 0:02:03
0:02:03
 0:00:06
0:00:06
 0:11:24
0:11:24
 0:00:17
0:00:17
 0:05:04
0:05:04
 0:05:02
0:05:02
 0:05:06
0:05:06
 0:08:09
0:08:09
 0:00:05
0:00:05