filmov
tv
How to Solve a Radical Equation with Golden Flavor
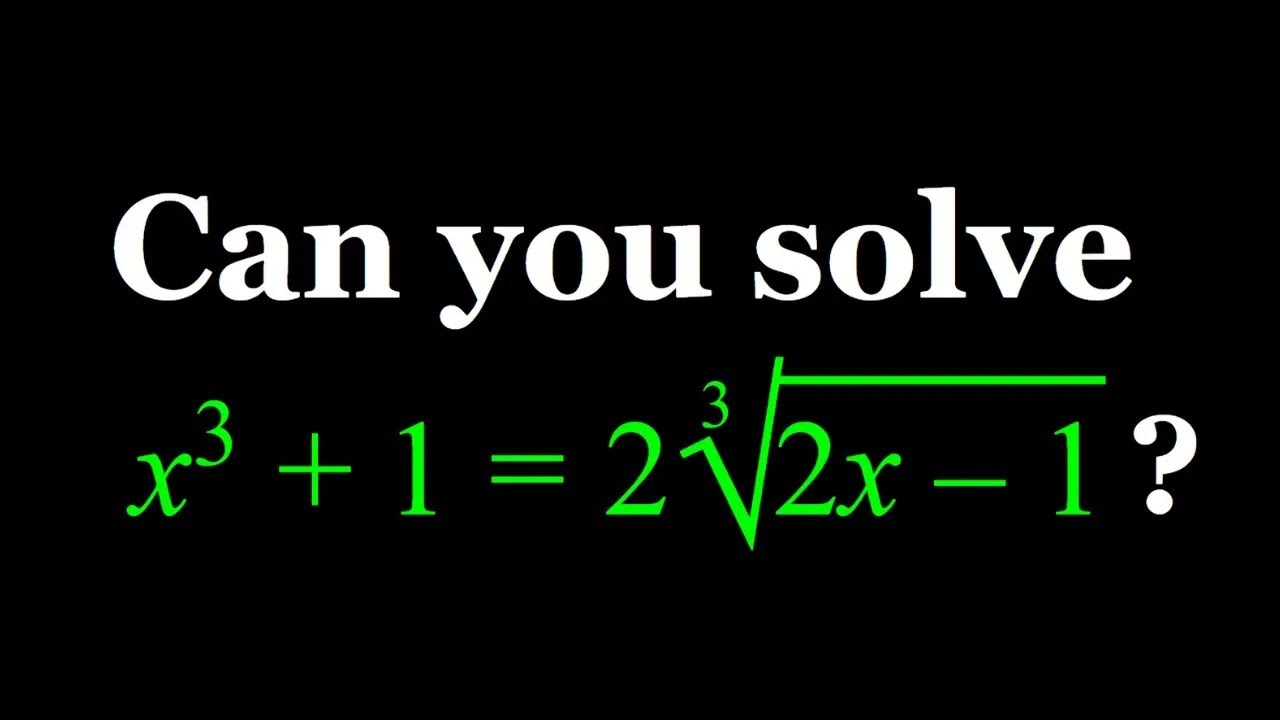
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#radicalequations #algebra #radicals
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#radicalequations #algebra #radicals
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Simplifying Radicals Easy Method
How To Simplify Radicals
Solving Radical Equations
Learn to add and subtract radical expressions
Simplify Radicals without Variables #math
Simplifying Radicals Easy Method
Solving Radical Equations With Square Roots, Cube Roots, Two Radicals, Fractions, Rational Exponents
Short Tricks on Square Root in 5 Seconds #shorttricks #shorttricksmaths #shorts
2025 Olympiads Exams || How to Solve for n? #maths
Adding and Subtracting Radical Expressions With Square Roots and Cube Roots
How To Simplify Square Roots
How to Simplify Radicals (NancyPi)
Learn How to Solve a Radical Equation and Check Your Answers
Learn how to simplify a radical
Pre-Algebra 31 - Simplifying Radical Expressions
How to Simplify Radicals #math #mathematics #mathstricks #maths
How to Solve a Radical Equation with two Square Root Terms
Simplify a radical expression with variables
How to Solve a Radical Equation with No Solution √(x-2) - 3 = -8
Solving radical equations | Exponent expressions and equations | Algebra I | Khan Academy
Solving a Radical Equation Using Factoring and Checking Your Answers
Solving Radical Equations - Solution of Radical Equations
#9. Solve the Radical Equation with Two Square Roots
How to Solve Radical Equations: Easy-to-Understand Method
Комментарии
 0:03:42
0:03:42
 0:13:14
0:13:14
 0:17:11
0:17:11
 0:03:41
0:03:41
 0:00:58
0:00:58
 0:03:06
0:03:06
 0:18:05
0:18:05
 0:00:45
0:00:45
 0:08:19
0:08:19
 0:11:20
0:11:20
 0:10:46
0:10:46
 0:17:51
0:17:51
 0:03:18
0:03:18
 0:04:09
0:04:09
 0:09:28
0:09:28
 0:01:00
0:01:00
 0:04:57
0:04:57
 0:05:14
0:05:14
 0:01:21
0:01:21
 0:03:11
0:03:11
 0:04:25
0:04:25
 0:10:01
0:10:01
 0:05:17
0:05:17
 0:05:37
0:05:37