filmov
tv
Can You Solve these If-Then Radical Equations? | Step-by-Step Explanation

Показать описание
Can You Solve these If-Then Radical Equations? | Step-by-Step Explanation
Can You Solve this If-Then Math Problem? | Math Challenge!
Can you solve This If-Then Algebraic Question? | Step-by-Step Explanation
Can You Solve this If-Then Math Problem? | Step-by-Step Tutorial
Can you solve this If Then Math Puzzle?
Can you solve this IF THEN MATH PUZZLE?
If You Solve 10% of These Riddles, You Are Better Than Sherlock
If Then Math Puzzle I Can you solve this?
Can you solve this If-Then Exponential Problem? | Fast & Easy Explanation
Can You Solve this If-Then Multivariable System of Equations Problem? | Step-by-Step Tutorial
Solve These Detective Riddles or Admit Defeat
Can You Solve this If-Then Problem? | Radicals & Negative Exponents!
If You Solve 20% of These Riddles, You Are Smarter Than Sherlock
🤔 If You Can Solve These Short Riddles Then You're Smart Enough For High School 👨🎓
Reborn, he stopped giving his all, dumped his toxic girlfriend, and married someone else.
Can you solve this? If You are not getting the answer then check the discription box👍👍
Can you solve this puzzle with only two pieces?#puzzle#iq#iqtest
The Second Punic War - OverSimplified (Part 3)
If You Solve These 21 Riddles, You're a Real Brainiac
If you are Intelligent, Solve these 6 Math Problems | How Smart are You?
If I Can't Solve These Puzzles, My Kids Will Punish Me
YOU'RE A GENIUS IF YOU CAN SOLVE THESE 17 DIFFICULT RIDDLES!
Solve this if you are genius!😱 #mathstest #iqtest #followformore
If you solve this then you are genius | IQ test 🧐🤓 #maths #shorts
Комментарии
 0:10:14
0:10:14
 0:06:11
0:06:11
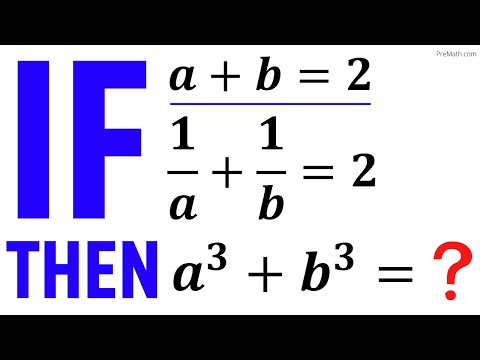 0:04:34
0:04:34
 0:04:38
0:04:38
 0:01:01
0:01:01
 0:01:01
0:01:01
 0:10:48
0:10:48
 0:01:01
0:01:01
 0:06:06
0:06:06
 0:10:55
0:10:55
 0:09:53
0:09:53
 0:08:05
0:08:05
 0:10:38
0:10:38
 0:14:46
0:14:46
 1:20:02
1:20:02
 0:00:12
0:00:12
 0:01:00
0:01:00
 0:49:06
0:49:06
 0:11:57
0:11:57
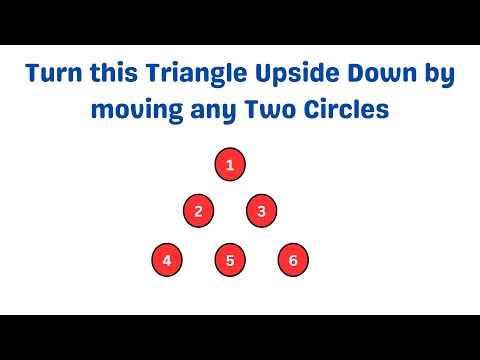 0:04:32
0:04:32
 0:10:33
0:10:33
 0:14:51
0:14:51
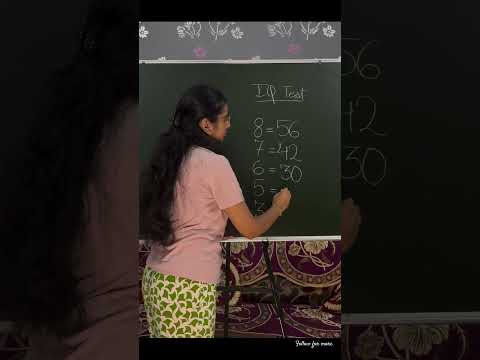 0:00:15
0:00:15
 0:00:11
0:00:11