filmov
tv
Solving a Radical Equation with Unlike Roots
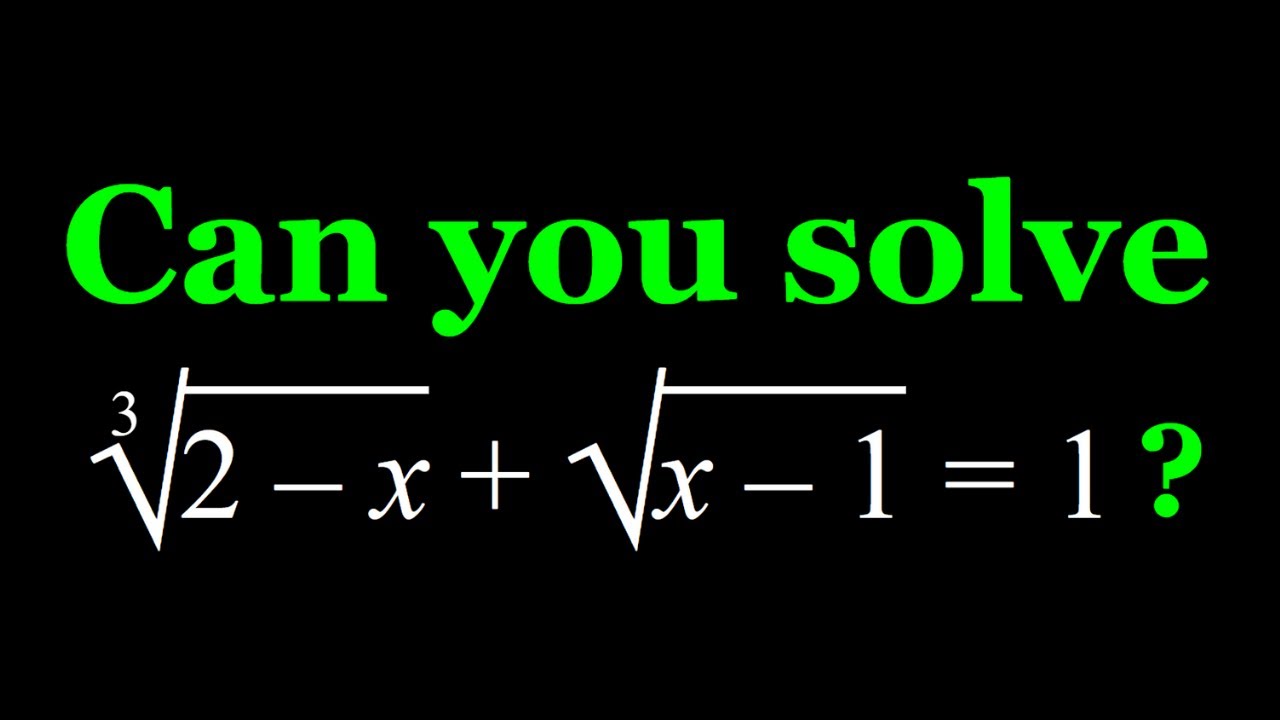
Показать описание
This video is about solving a complicated radical equation
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #RadicalEquations
EXPLORE:
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #RadicalEquations
EXPLORE:
Solving Radical Equations
Solving Radical Equations With Square Roots, Cube Roots, Two Radicals, Fractions, Rational Exponents
Solving radical equations | Exponent expressions and equations | Algebra I | Khan Academy
Solving a Radical Equation Using Factoring and Checking Your Answers
Solve Radical (Square Root) Equations with Two Radicals
Solving Radical Equations
#9. Solve the Radical Equation with Two Square Roots
Learn How to Solve a Radical Equation and Check Your Answers
Subtraction of radicals: √150- √ 54 #governmentexam #radical #civilexam
Math Tutorial for Solving Radical Equations
Solving Radical Equations (More Challenging)
How to Solve Radical Equations that have Two Radicals - Simple Method
How to Solve Radical Equation with Two Radicals?
Solving an Equation Containing Two Radicals - Example 1
How to solve a radical equation by using rational powers using absolute value
Solving Radical Equations - Solution of Radical Equations
Solving an Equation with the Difference of Two Radical Expressions
Solving Radical Equations | SHS 1 ELECTIVE MATH
05 - Solving Radical Equations & Identifying Extraneous Solutions - Part 1
Radical Equation with a Extraneous Solution
Checking For Extraneous Solutions of Radical Equations
The most important thing you need to know to solve radical equations
Solving A Nice Radical Equation | How To Solve Radical Equation With Two Radicals.
How to Solve an Equation with a Radical Expression on Both Sides
Комментарии
 0:17:11
0:17:11
 0:18:05
0:18:05
 0:03:11
0:03:11
 0:04:25
0:04:25
 0:09:31
0:09:31
 0:03:31
0:03:31
 0:05:17
0:05:17
 0:03:18
0:03:18
 0:00:46
0:00:46
 0:03:45
0:03:45
 0:04:14
0:04:14
 0:08:23
0:08:23
 0:05:45
0:05:45
 0:04:37
0:04:37
 0:07:38
0:07:38
 0:10:01
0:10:01
 0:06:00
0:06:00
 0:11:48
0:11:48
 0:27:27
0:27:27
 0:05:11
0:05:11
 0:10:22
0:10:22
 0:03:42
0:03:42
 0:19:51
0:19:51
 0:01:28
0:01:28