filmov
tv
Simplifying a Golden Radical Expression in Three Ways

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #RadicalExpressions
CHECK IT OUT 😊:
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #RadicalExpressions
CHECK IT OUT 😊:
EXPLORE 😎:
PLAYLISTS 🎵 :
Simplifying a Golden Radical Expression in Three Ways
Simplifying a Golden Radical Expression in Two Ways
Simplifying a Quick and Easy Radical Expression
Solving a Golden Radical Equation
A Golden Radical Equation
Simplifying A Radical Expression | Three Methods
Simplifying A Very Radical Expression | Denesting Radicals
Simplify Radical Expressions Three Different Ways
Simplifying a Radical Expression in Two Ways
An Infinite Radical Expression | The Golden Ratio
Simplifying a Radical Expression in Three Ways
Steps oh How To Simplify Expression Under the Radical Sign | Math Tutorial
Simplifying Radical Expressions II (2020 DL)
A Golden Radical and Powers of Golden Ratio
Simplify this Radical Expression | Step-by-Step Explanation
Simplifying A Radical | Math Olympiads
An Infinite Radical with A Golden Flavor
Radical Expressions Made Easy : Radical Numbers
Math - Simplifying Radicals
Simplifying sqrt(2021*2025+4), a Radical Expression
Simplifying a Tough Radical Expression
Ex: Simplify a Radical Expression containing Square Roots in the Numerator and Denominator
A Golden Radical Expression ...|| A Nice Simplification ....|| Easy to Solve ...math903
USA IMO Training Problem | Simplifying a Trigonometric Radical Expression | Pythagorean Identity
Комментарии
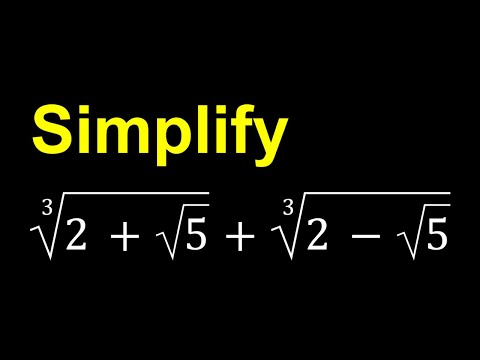 0:10:55
0:10:55
 0:12:35
0:12:35
 0:05:01
0:05:01
 0:13:50
0:13:50
 0:00:33
0:00:33
 0:08:52
0:08:52
 0:08:43
0:08:43
 0:09:07
0:09:07
 0:04:50
0:04:50
 0:09:33
0:09:33
 0:08:31
0:08:31
 0:00:54
0:00:54
 0:07:28
0:07:28
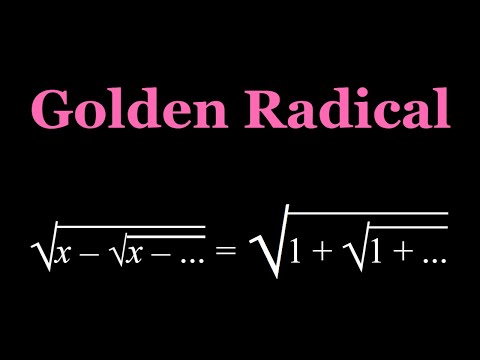 0:09:06
0:09:06
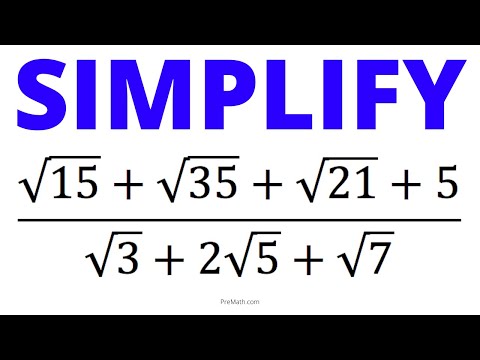 0:14:47
0:14:47
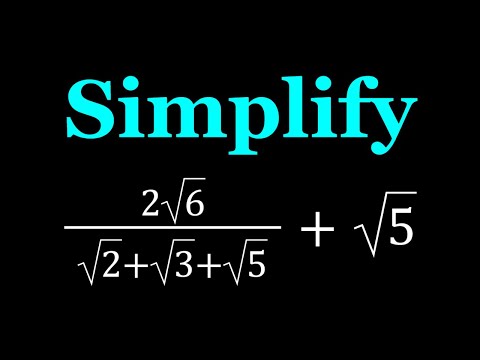 0:08:16
0:08:16
 0:00:41
0:00:41
 0:02:44
0:02:44
 0:10:14
0:10:14
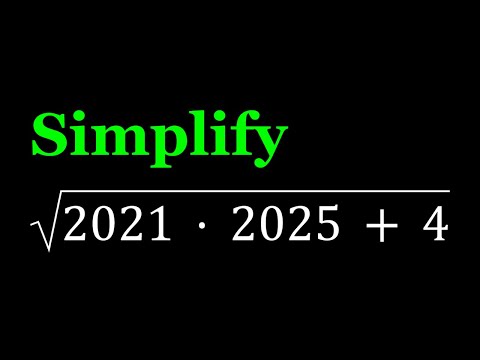 0:03:20
0:03:20
 0:13:12
0:13:12
 0:03:13
0:03:13
 0:03:38
0:03:38
 0:04:50
0:04:50