filmov
tv
Solving a septic equation

Показать описание
In this video, I solved a septic equation by considering a pattern of factors in the difference of polynomials of higher degrees
Get your t-shirt here:
The Quality of this shirt is impressive. You will also be helping me a lot!
Colors: Black, Navy Blue, Gray, Red.
Get your t-shirt here:
The Quality of this shirt is impressive. You will also be helping me a lot!
Colors: Black, Navy Blue, Gray, Red.
Solving a septic equation
Let's Solve A Special Septic Equation | Polynomials
Simple Way to Solve the Septic Polynomial Equation 16x^7+7x^3+1=0
Evaluating A Septic Algebraic Expression
Factoring a Septic Polynomial | Algebra Challenge
Solving a quartic equation using an unusual idea. An algebraic challenge.
Can We Solve A Septic, I Mean A Heptic 😄
An Ecuador Olympiad Challenge | Crack This Septic Equation
Are You in the 5%? Master the Septic Equation Test!
#septic_equation Solve X⁷=X | How To Solve a Septic Equation | Problems On Algebra | JMO
Solving a Heptic Equation Without Using the Heptic Formula
Solving Polynomial Equations - Grade 10 Math
Evaluating a Septic Algebraic Expression in Three Ways
How to solve the quartic equation by the Ferrari method?
Solving an equation in non-standard ways
Can We Solve A Septic, I Mean A Heptic 😄 I A-MATHS
A quartic equation that can be solved easily. No quartic formula needed.
Solving A Real Polynomial System in Two Ways
Solving a Nice Cubic System in Two Ways
Solving a quartic equation with parameters
Solving a Non-standard System of Equations
Solving a Nice Radical System in Two Ways
Factoring a tenth degree polynomial. An algebraic challenge solved in two ways.
Solving a very radical equation using a non-standard method. An algebraic challenge...
Комментарии
 0:10:43
0:10:43
 0:08:57
0:08:57
 0:02:12
0:02:12
 0:09:14
0:09:14
 0:09:43
0:09:43
 0:17:05
0:17:05
 0:09:22
0:09:22
 0:09:04
0:09:04
 0:10:16
0:10:16
 0:06:39
0:06:39
 0:09:22
0:09:22
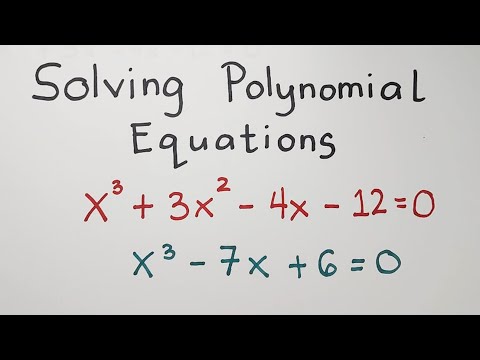 0:12:02
0:12:02
 0:10:48
0:10:48
 0:13:19
0:13:19
 0:16:41
0:16:41
 0:01:44
0:01:44
 0:05:52
0:05:52
 0:10:59
0:10:59
 0:09:13
0:09:13
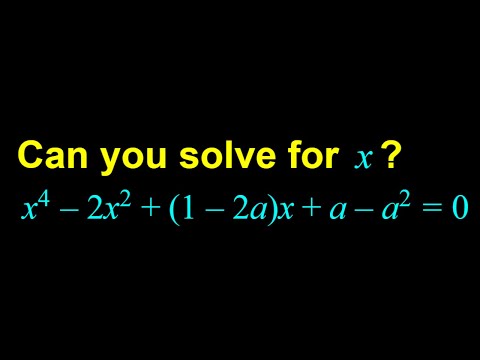 0:11:26
0:11:26
 0:10:17
0:10:17
 0:09:12
0:09:12
 0:13:34
0:13:34
 0:06:54
0:06:54