filmov
tv
a functional equation

Показать описание
We look at a functional equation problem that was shortlisted for the 1995 International Mathematics Olympiad.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
A Quick and Easy Functional Equation
A Functional Equation from Samara Math Olympiads
Learn Functions – Understand In 7 Minutes
Functional Equation
A Nice and Easy Functional Equation
A Functional Equation with Golden Flavor
the greatest functional equation of all time.
Methods of Functional Equations
A functional equation from my favorite book.
A Functional Equation from British Math Olympiads 2009
Solving a Functional Equation
a functional equation
a fun functional equation
A Functional Equation from Putnam and Beyond
A fun functional equation!!
A Nice and Easy Functional Equation
Determine if the equation represents a function
a notorious functional equation.
an absolutely surprising final solution to this functional equation.
A Basic Functional Equation
A functional equation from @goodplacetostop2973
A functional equation from the Philippines.
A Curious Functional Equation | Math Olympiads
A Functional Equation from Türkiye 🇹🇷
Комментарии
 0:06:49
0:06:49
 0:08:47
0:08:47
 0:09:43
0:09:43
 0:14:15
0:14:15
 0:05:07
0:05:07
 0:07:21
0:07:21
 0:07:48
0:07:48
 0:07:40
0:07:40
 0:11:23
0:11:23
 0:08:33
0:08:33
 0:10:36
0:10:36
 0:16:24
0:16:24
 0:09:20
0:09:20
 0:12:07
0:12:07
 0:11:13
0:11:13
 0:08:14
0:08:14
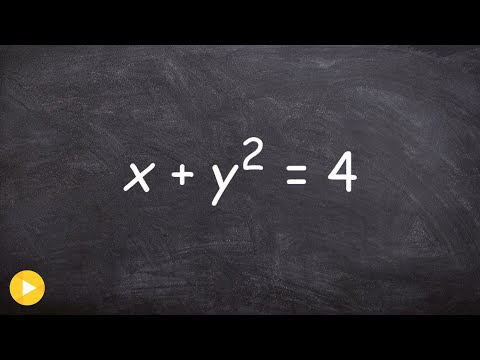 0:02:14
0:02:14
 0:19:30
0:19:30
 0:18:15
0:18:15
 0:07:30
0:07:30
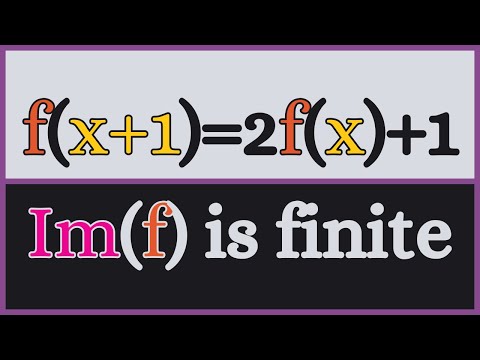 0:08:18
0:08:18
 0:07:44
0:07:44
 0:08:29
0:08:29
 0:08:55
0:08:55