filmov
tv
Germany Math Olympiad, a system of cubic equations
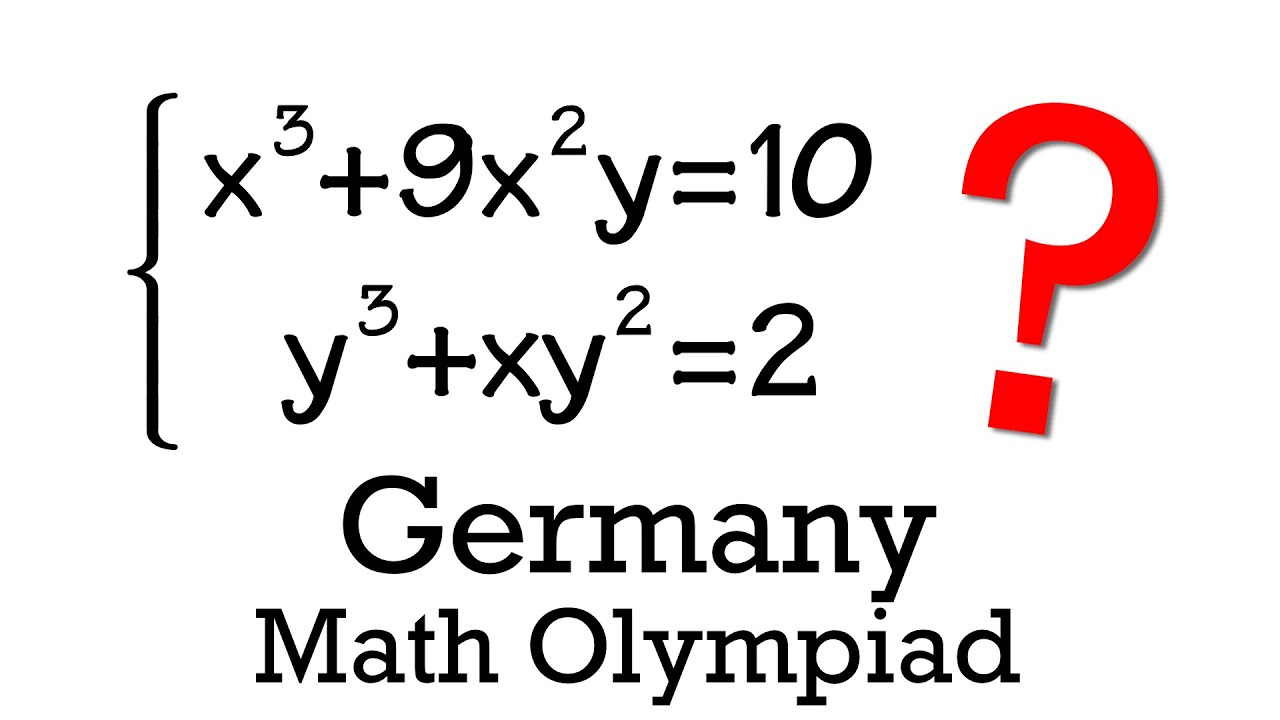
Показать описание
This question is question 1 from the 2015 Germany math olympiad contest. I love the fun and creative system of equations!
Subscribe for more math for fun videos 👉 @blackpenredpen
Subscribe for more math for fun videos 👉 @blackpenredpen
Germany Math Olympiad, a system of cubic equations
A nice problem from the 1972 German math Olympiad
Solving a System of Equations from Germany | German Math Olympiad Problem | Can You Solve This?
Luxembourg - Math Olympiad Question | You should know this trick
Germany Math Olympiad Question | You should know this trick!
Norway Math Olympiad Question | You should be able to solve this!
2015 German Math Olympiad
A Surprisingly Easy National Maths Olympiad Problem | German MO 2015
Germany || Can You Solve This? A Nice Math Olympiad Exponential Equation Problem
German Maths Olympiad is Absolutely Wild
Germany Math Olympiad Problem | A Very Nice Geometry Challenge
Germany| Can you solve this? | A math Olympiad exponential problem
Learn How To Solve a German Math Olympiad!@AyaansMath
Germany - Math Olympiad Question | The BEST Trick
Learn How To Solve a German Math Olympiad: From The Experts!
Awesome Algebra!System of Equations-German Math Olympiad
Russia | Math Olympiad Question | You should know this trick!!
Germany | A Nice Math Olympiad Problem.
hard Germany mathematical Olympiad
Germany - Math Olympiad Challenge | Solve for integers a,b
Olympiad Mathematics | Learn How to Solve the System of Equations Fast | Math Olympiad Preparation
Germany | Math Olympiad | You should know this trick to solve
Learn How To Solve a German Math Olympiad 2!@AyaansEasyMath
Germany - Math Olympiad Exponential Problem
Комментарии
 0:11:36
0:11:36
 0:13:10
0:13:10
 0:08:13
0:08:13
 0:02:51
0:02:51
 0:11:10
0:11:10
 0:03:21
0:03:21
 0:09:11
0:09:11
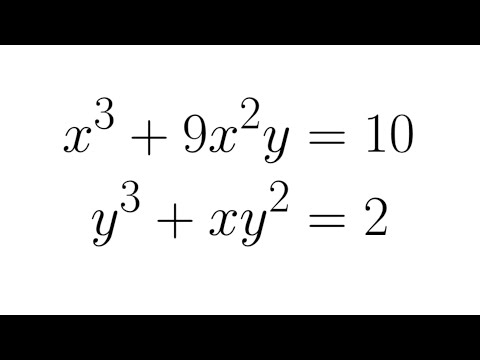 0:04:24
0:04:24
 0:08:00
0:08:00
 0:16:44
0:16:44
 0:14:50
0:14:50
 0:13:32
0:13:32
 0:11:41
0:11:41
 0:10:37
0:10:37
 0:09:27
0:09:27
 0:09:23
0:09:23
 0:08:01
0:08:01
 0:06:14
0:06:14
 0:12:14
0:12:14
 0:04:25
0:04:25
 0:06:26
0:06:26
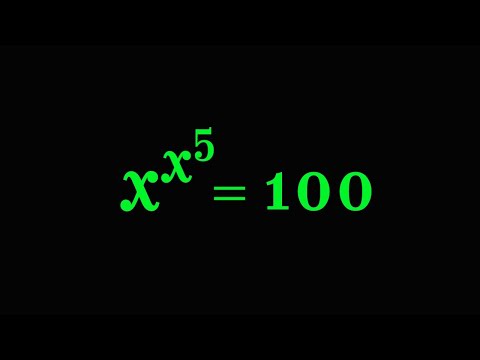 0:03:08
0:03:08
 0:08:57
0:08:57
 0:04:46
0:04:46