filmov
tv
A Cubic System of Equations

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#Algebra #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#Algebra #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
A Cubic System of Equations
A cubic system of equations
Solving a Cubic System
Solving a cubic system
Germany Math Olympiad, a system of cubic equations
Solving a cubic system for real solutions
Solving a Cubic System for Real Solutions
Solving a cubic equation
Can You Solve This BEAUTIFUL Exponential Equation?
Solving a Nice Cubic System in Two Ways
A Cubic Polynomial System
Solving a Cubic Polynomial in Two Ways
Solve the Nonlinear System: A Cubic Polynomial and a Line
Solving a cubic system of equation
Let's Solve A Cool Cubic System
Solving a Cubic System in a Non-polynomial Way
The Linear-Cubic System. THE MOST GENERAL SOLUTION. | System of Equations
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
Solving A Special Cubic System in Two Ways
German Math Olympid | How to solve this cubic system of equations | Simple and easy solution
A Nice Cubic Equation - Number Theory | Advanced Math
Solving a Cubic Equation - √(X^3) = 1
Solving a cubic equation with irrational coefficients. A radical challenge in algebra.
Solving A Cubic Equation With An Irrational Root
Комментарии
 0:13:25
0:13:25
 0:13:25
0:13:25
 0:14:14
0:14:14
 0:14:14
0:14:14
 0:11:36
0:11:36
 0:09:15
0:09:15
 0:09:15
0:09:15
 0:07:26
0:07:26
 0:08:56
0:08:56
 0:09:13
0:09:13
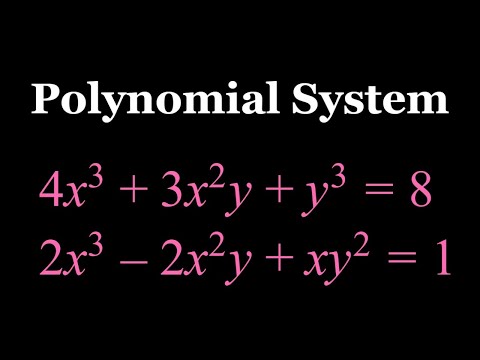 0:10:31
0:10:31
 0:09:55
0:09:55
 0:08:17
0:08:17
 0:10:10
0:10:10
 0:09:13
0:09:13
 0:09:29
0:09:29
 0:08:54
0:08:54
 0:10:52
0:10:52
 0:14:48
0:14:48
 0:05:33
0:05:33
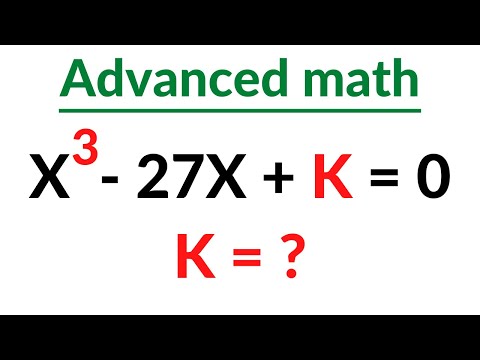 0:08:36
0:08:36
 0:00:58
0:00:58
 0:06:36
0:06:36
 0:16:23
0:16:23