filmov
tv
An inductive proof of Fermat's little theorem.
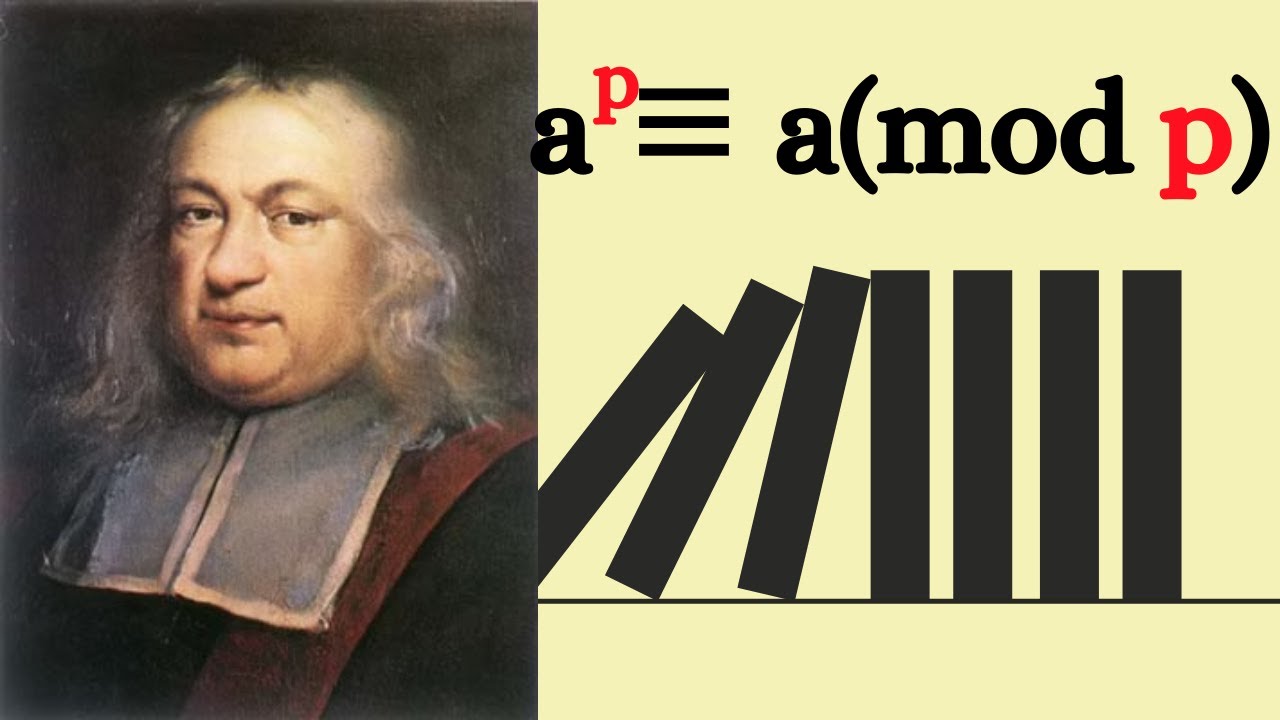
Показать описание
We give a nice proof of Fermat's little theorem using induction.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
An inductive proof of Fermat's little theorem.
A Gentle Proof of Fermat's Little Theorem by Induction
Proof of Fermat's Little Theorem using Induction
Fermat's Little Theorem - Proof by Mathematical Induction
My new favorite proof of Fermat's little theorem!!
Proving weird Fermat's Last Theorem in just 2 minutes !
Fermat's Little Theorem - Explained in 5 minutes!
Fermat's Last Theorem: A Very, Very Basic Proof
What was Fermat’s “Marvelous' Proof? | Infinite Series
INCORRECT PROOF of Fermat's Last Theorem
Fermat's Theorem in Bedazzled | Math in Movies
Pingu reacting to proof of Fermat's Last Theorem
Fermat's Little Theorem - Simple Intuitive Proof
Andrew Wiles: Fermat's Last theorem: abelian and non-abelian approaches
Applying Fermat's Little Theorem
A Gentle Proof of Fermat's Little Theorem and Fermat-Euler Theorem
How Was Fermat's Last Theorem Proved for Regular Primes?
Fermat's Little Theorem | A Proof of Fermat's Little Theorem from Number Theory
Fermat's Proof - Why You can never have a right triangle with a square area
FERMAT’S LAST THEOREM PROVED BY INDUCTION (accompanied by a philosophical comment)
Use Fermat Numbers to Prove the Infinitude of Prime Numbers
Kenneth A. Ribet, 'A 2020 View of Fermat's Last Theorem'
Fermat's Little Theorem Examples
An Application of Fermat's Last Theorem
Комментарии
 0:07:35
0:07:35
 0:10:30
0:10:30
 0:09:06
0:09:06
 0:05:28
0:05:28
 0:15:44
0:15:44
 0:02:00
0:02:00
 0:05:18
0:05:18
 0:05:00
0:05:00
 0:14:40
0:14:40
 0:10:20
0:10:20
 0:00:55
0:00:55
 0:00:10
0:00:10
 0:06:55
0:06:55
 0:53:12
0:53:12
 0:02:16
0:02:16
 0:11:42
0:11:42
 0:17:05
0:17:05
 0:11:03
0:11:03
 0:01:14
0:01:14
 0:05:07
0:05:07
 0:07:05
0:07:05
 0:52:21
0:52:21
 0:04:21
0:04:21
 0:05:47
0:05:47