filmov
tv
Fermat's Little Theorem - Explained in 5 minutes!

Показать описание
Fermat's Little Theorem can help us find the remainder when a very large number is divided by a prime number.
Fermat's Little Theorem
Fermat's Little Theorem - Explained in 5 minutes!
Fermat's Little Theorem ← Number Theory
Fermat's little theorem | Journey into cryptography | Computer Science | Khan Academy
Applying Fermat's Little Theorem
Number Theory | Fermat's Little Theorem
Proving Fermat' s Last Theorem (almost) in just 2 minutes !
Fermat’s HUGE little theorem, pseudoprimes and Futurama
Fermat's Little Theorem (Visualization)
Euler's Totient Theorem and Fermat's Little Theorem - Complete Proof & Intuition
Fermat's Little Theorem and Euler's Totient Theorem/Function
Number Theory | Fermat's Little Theorem Example 1
Fermat's Last Theorem - Numberphile
Fermat's Little Theorem examples
Proof of Fermat's Little Theorem
An inductive proof of Fermat's little theorem.
My new favorite proof of Fermat's little theorem!!
FERMATS LITTLE THEOREM EXPLAINED
Fermat's Little Theorem
Solving Fermat's Little Theorem The Easy Way.😀
Fermat's Little Theorem | A Proof of Fermat's Little Theorem from Number Theory
Fermat’s Little Theorem with examples
Fermat's Little Theorem - Proof by Mathematical Induction
Fermat's Theorem Numerical examples | Important for exams
Комментарии
 0:07:31
0:07:31
 0:05:18
0:05:18
 0:10:35
0:10:35
 0:06:06
0:06:06
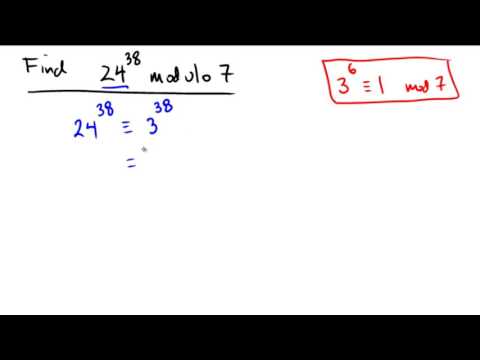 0:02:16
0:02:16
 0:06:14
0:06:14
 0:02:00
0:02:00
 0:18:40
0:18:40
 0:06:06
0:06:06
 0:15:29
0:15:29
 0:03:53
0:03:53
 0:05:14
0:05:14
 0:09:31
0:09:31
 0:11:45
0:11:45
 0:07:25
0:07:25
 0:07:35
0:07:35
 0:15:44
0:15:44
 0:06:36
0:06:36
 0:19:16
0:19:16
 0:08:42
0:08:42
 0:11:03
0:11:03
 0:06:05
0:06:05
 0:05:28
0:05:28
 0:03:46
0:03:46