filmov
tv
Solving sqrt(1+sqrt(x)) = x-1in Two Ways

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #RadicalEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #RadicalEquations
PLAYLISTS 🎵 :
Solving sqrt(1+sqrt(x)) = x-1in Two Ways
sqrt(x-1)sqrt(4-x^2) = sqrt(x^2-1)sqrt(4-x)
Solving x^sqrt(x)=1/2, an Exponential Equation
Solving x^(1/x)=sqrt(2), a Homemade Exponential Equation
Solving x^{1/sqrt(x)}=1/16
Working with an Exponential Expression in Three Ways
An Infinite Series Under The Radical
Solving a very radical equation. An algebraic challenge.
Solving A Nice Cubic System in Two Ways
Simplifying sqrt(2021*2025+4), a Radical Expression
Comparing log_10(11) and log_11(12)
Solving A Real Polynomial System in Two Ways
Solving an equation with a cubic root and a square root. This is too radical!!!
Solving a Non-standard System of Equations
Evaluating a Septic Algebraic Expression in Three Ways
Solving a Radical Exponential Equation
Solving x^{sqrt(logx)}=10^8 in Two Ways
Evaluating A Radical Expression with Cardano's Formula
Evaluating x+(5/sqrt(x)) when x+sqrt(x)=5
Solving Inverse of xe^x function using Approximations by Differentials | Math Videos
Simplify expression sqrt(9+ sqrt(72)) - sqrt(9 - sqrt(72)). Advanced Factoring
Evaluating an Algebraic Expression from a Radical Equation
V3-09. Linear Programming. introduction to Simplex method. Step 4.
Solving 37tan3x = 11tanx
Комментарии
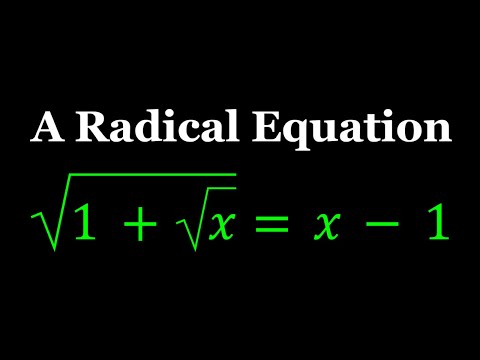 0:11:29
0:11:29
 0:02:53
0:02:53
 0:09:57
0:09:57
 0:09:05
0:09:05
 0:10:36
0:10:36
 0:09:23
0:09:23
 0:09:42
0:09:42
 0:12:51
0:12:51
 0:09:41
0:09:41
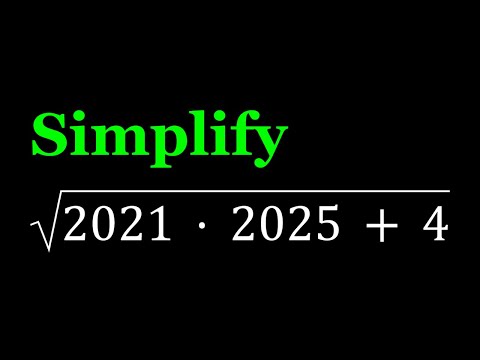 0:03:20
0:03:20
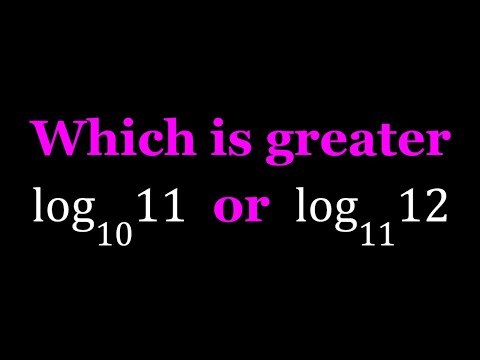 0:09:29
0:09:29
 0:10:59
0:10:59
 0:11:55
0:11:55
 0:10:17
0:10:17
 0:10:48
0:10:48
 0:05:05
0:05:05
 0:05:06
0:05:06
 0:11:49
0:11:49
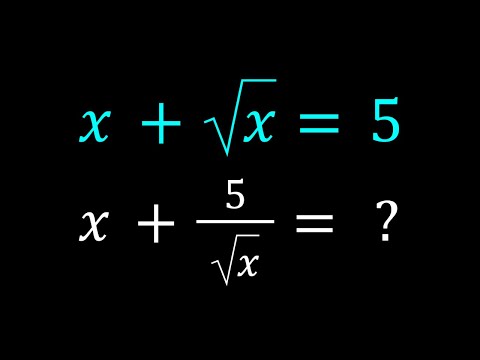 0:08:15
0:08:15
 0:01:00
0:01:00
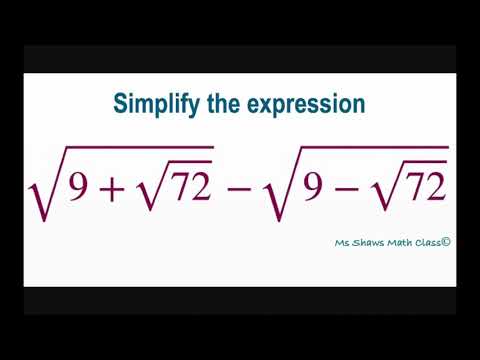 0:03:22
0:03:22
 0:06:53
0:06:53
 0:16:43
0:16:43
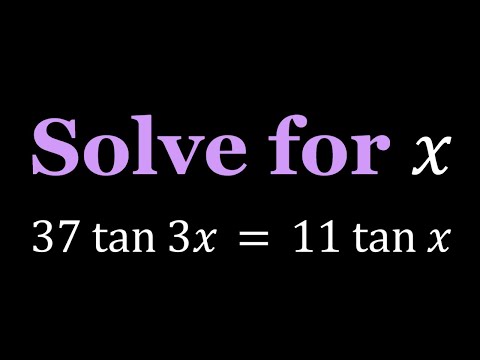 0:10:00
0:10:00