filmov
tv
Solving an equation with a cubic root and a square root. This is too radical!!!
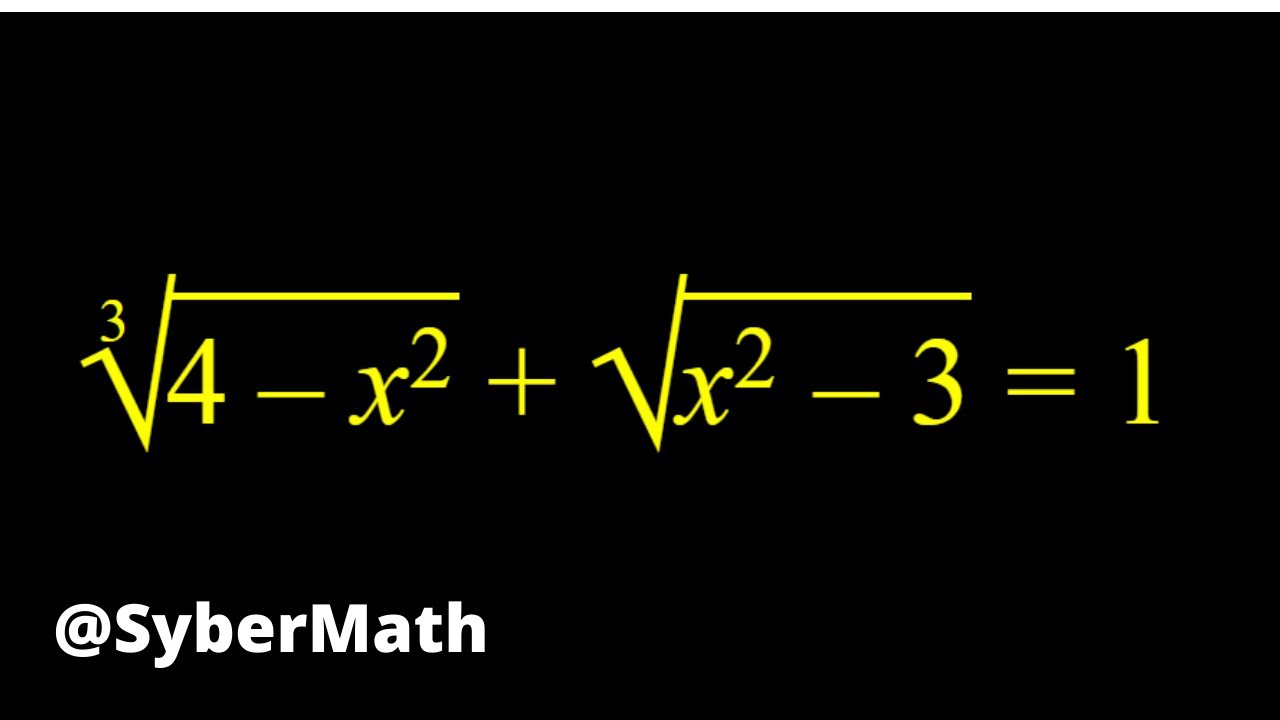
Показать описание
This video is about solving an equation that has a cubic root and a square root in it.
Solving an equation with variables on both side and one solution
Solve the equation
How to Solve One-Step Equations | One-Step Equation Steps | Math with Mr. J
Introduction to solving an equation with variables on both sides | Algebra I | Khan Academy
Solve quadratic equation by factorisation
Solving an equation for y and x using two steps
Solving an equation for y and x
Solving an Equation for a Specified Variable
Algebra 1 Review Solve Equations and Inequalities
Solve the simultaneous equation ECZ
Solving an equation with variable on both sides No Solution
Solving a literal equation with a rational term
Solve the simultaneous equation
Linear Equation | Solving Linear Equations
Solving an Equation
Solving Exponential Equation
How To Solve Absolute Value Equations, Basic Introduction, Algebra
Elimination Method For Solving Systems of Linear Equations Using Addition and Multiplication, Algebr
Quadratic Equation Shortcut Trick | Solve Equation in 5 Seconds
Solving a one step equation with a mixed number
Solving an equation by quadratic formula
Linear Equations - Algebra
Solve an equation for x by clearing fractions with multiple steps
Solving an equation by combining like terms
Комментарии
 0:02:36
0:02:36
 0:01:53
0:01:53
 0:06:54
0:06:54
 0:08:53
0:08:53
 0:09:05
0:09:05
 0:03:12
0:03:12
 0:03:47
0:03:47
 0:03:58
0:03:58
 0:17:02
0:17:02
 0:01:38
0:01:38
 0:02:47
0:02:47
 0:03:39
0:03:39
 0:04:11
0:04:11
 0:11:20
0:11:20
 0:05:21
0:05:21
 0:00:56
0:00:56
 0:04:21
0:04:21
 0:10:21
0:10:21
 0:00:30
0:00:30
 0:02:56
0:02:56
 0:04:13
0:04:13
 0:32:05
0:32:05
 0:03:44
0:03:44
 0:02:45
0:02:45