filmov
tv
Solving a very radical equation. An algebraic challenge.
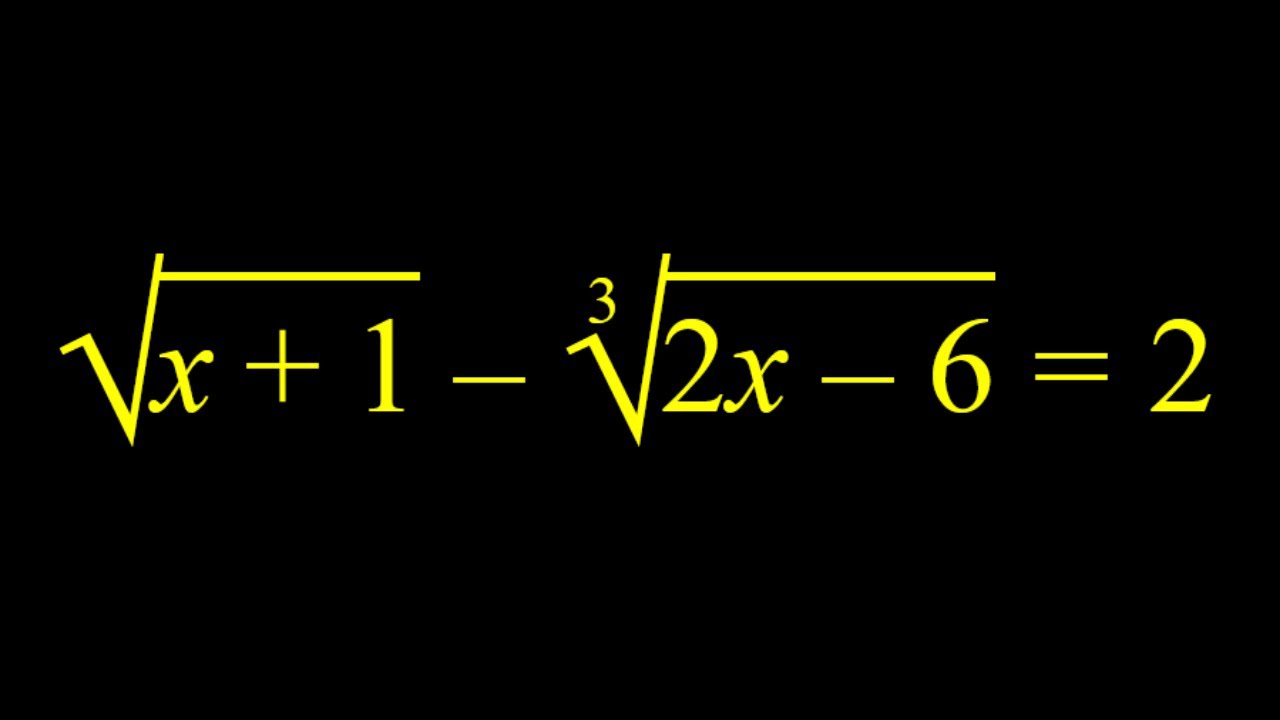
Показать описание
This video is about solving a radical equation. See what happens if you square both sides.
Radical expressions,algebra,algebraic equations,SyberMath,algebraic manipulations,equations,substitution,Challenging Math Problems,Non-routine Math Problems,polynomial equations,an algebra challenge,algebraic identities,non-standard methods,symmetry,math,maths,mathematics,An algebraic challenge,Polynomial equations,an algebraic challenge,an equation,cubic equations,power of substitution,systems of equations,quadratic formula,Solving a very radical equation
Radical expressions,algebra,algebraic equations,SyberMath,algebraic manipulations,equations,substitution,Challenging Math Problems,Non-routine Math Problems,polynomial equations,an algebra challenge,algebraic identities,non-standard methods,symmetry,math,maths,mathematics,An algebraic challenge,Polynomial equations,an algebraic challenge,an equation,cubic equations,power of substitution,systems of equations,quadratic formula,Solving a very radical equation
Solving Radical Equations
solving a very radical equation
Solving Radical Equations With Square Roots, Cube Roots, Two Radicals, Fractions, Rational Exponents
Solving radical equations | Exponent expressions and equations | Algebra I | Khan Academy
Solving a very radical equation. An algebraic challenge.
Can We Solve A Very Radical Equation | Problem 151
Solving a very radical equation using a non-standard method. An algebraic challenge...
Solving a Radical Equation Using Factoring and Checking Your Answers
A Nice Radical Equation | Using The Factorisation Method.
Solving Radical Equations
Solving A Radical Equation Using a Radical Method (maybe)
05 - Solving Radical Equations & Identifying Extraneous Solutions - Part 1
Solving an Equation Containing Two Radicals - Example 1
A Very Radical Equation Solved in Two Ways
Learn How to Solve a Radical Equation and Check Your Answers
Solve Radical (Square Root) Equations with Two Radicals
The most important thing you need to know to solve radical equations
#9. Solve the Radical Equation with Two Square Roots
Math Tutorial for Solving Radical Equations
How to Solve Radical Equations that have Two Radicals - Simple Method
Example: Solving a Radical Equation (Square Twice)
Solving a radical equation with a parameter
Radical Equation with a Extraneous Solution
Solving Radical Equations (More Challenging)
Комментарии
 0:17:11
0:17:11
 0:03:32
0:03:32
 0:18:05
0:18:05
 0:03:11
0:03:11
 0:12:51
0:12:51
 0:08:14
0:08:14
 0:06:54
0:06:54
 0:04:25
0:04:25
 0:06:12
0:06:12
 0:03:31
0:03:31
 0:08:07
0:08:07
 0:27:27
0:27:27
 0:04:37
0:04:37
 0:10:01
0:10:01
 0:03:18
0:03:18
 0:09:31
0:09:31
 0:03:42
0:03:42
 0:05:17
0:05:17
 0:03:45
0:03:45
 0:08:23
0:08:23
 0:04:52
0:04:52
 0:09:14
0:09:14
 0:05:11
0:05:11
 0:04:14
0:04:14