filmov
tv
Working with an Exponential Expression in Three Ways
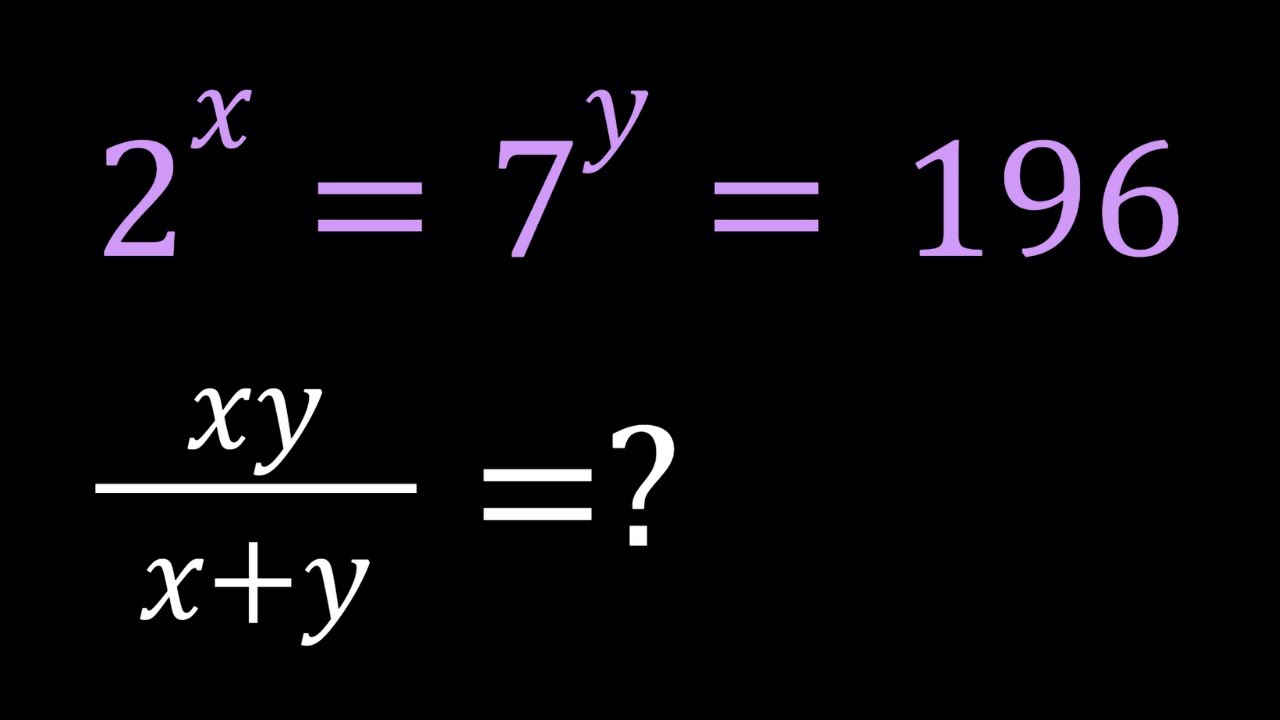
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialExpressions #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #ExponentialExpressions #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving Exponential Equations
Exponential growth functions | Exponential and logarithmic functions | Algebra II | Khan Academy
Algebra Basics: Laws Of Exponents - Math Antics
Simplifying Exponents With Fractions, Variables, Negative Exponents, Multiplication & Division, ...
Simplifying an exponential expression | Algebra II | Khan Academy
Exponential Equations - Algebra and Precalculus
What is an Exponent? | An Intro to Exponents | Math with Mr. J
Understanding Exponential Functions and their Gradients: Intuitive Approach
Exponential equation | High school students can solve.
Introduction to Exponential Functions - Nerdstudy
Working with an Exponential Expression in Three Ways
How do you solve an exponential equation with e as the base
What are exponential functions
Working with an Exponential System
Solving Exponential Equation
Negative Exponents Explained!
Finding a formula for an exponential function from a table
Logarithms, Explained - Steve Kelly
Fractional Exponents
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Exponential Equation Grade 10
MCR3U - Simplifying Complex Exponential Expressions Part 1 - Grade 11 Functions
What Is The Zero Exponent Rule Explained - Zero As An Exponent - A Number Raised To 0, Zero
07 - What is an Exponential Function? (Exponential Growth, Decay & Graphing).
Комментарии
 0:16:36
0:16:36
 0:07:41
0:07:41
 0:13:46
0:13:46
 0:11:48
0:11:48
 0:05:09
0:05:09
 0:05:58
0:05:58
 0:07:21
0:07:21
 0:08:10
0:08:10
 0:02:12
0:02:12
 0:03:22
0:03:22
 0:09:23
0:09:23
 0:02:47
0:02:47
 0:02:16
0:02:16
 0:08:36
0:08:36
 0:00:56
0:00:56
 0:12:38
0:12:38
 0:04:13
0:04:13
 0:03:34
0:03:34
 0:11:32
0:11:32
 0:00:52
0:00:52
 0:01:39
0:01:39
 0:07:53
0:07:53
 0:00:54
0:00:54
 0:45:07
0:45:07