filmov
tv
Solving 37tan3x = 11tanx
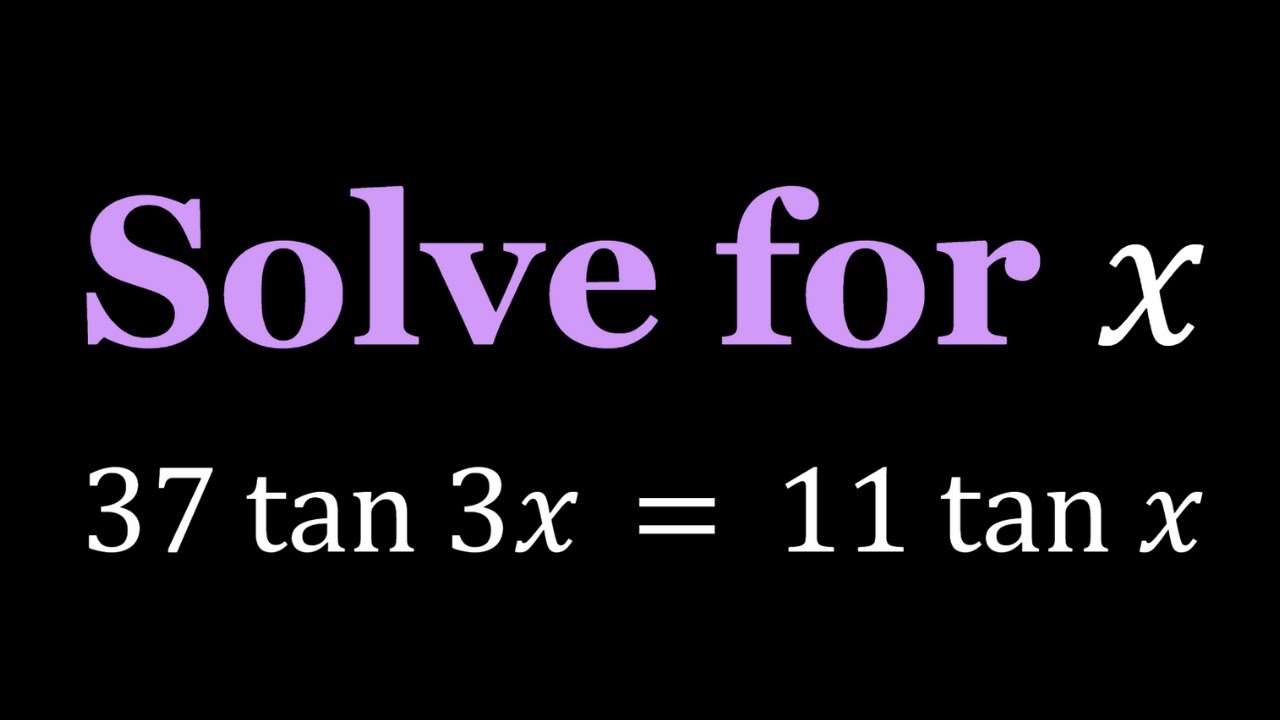
Показать описание
If you need to post a picture of your solution or idea:
#TrigonometryProblems #TrigonometricEquations
PLAYLISTS 🎵 :
#TrigonometryProblems #TrigonometricEquations
PLAYLISTS 🎵 :
Solving 37tan3x = 11tanx
Solving A Homemade Infinite Radical Equation
Random Math Problem (Trigo)
Solving A Real Polynomial System in Two Ways
Solving x^3 + 3x = 2i
Solving a system of equations using a famous trick
Evaluating a Polynomial Expression in Two Ways
A Polynomial System Inspired by Saratov Math Olympiads
Solving sin^2x+cos^3x=7/8
a very nice equation to solve
A Ratio of Two Infinite Series...
Solving x^(1/x)=sqrt(2), a Homemade Exponential Equation
Solving sqrt(1+sqrt(x)) = x-1in Two Ways
Evaluating A Radical Expression with Cardano's Formula
Evaluating a Logarithmic Expression in Three Ways
Finding tanα if tan(α+β)=7 and tan(α-β)=5
Comparing 5^23 and 7^15
Simplifying sqrt(17-4sqrt(9+4sqrt(5)))
Solving 7x^5+x+8 without Using the Quintic Formula
If A+B+C=180⁰ then prove that:- sin 6B + sin 6C - sin 6A = 4sin 3A.cos 3B. cos 3C.
Solving y^2+(y')^2=1
Solving The Pell's Equation (x^2-dy^2=1)
Solving xlnx=e
If sin A=2.511x, cos A=3.06x and sin 2A=3.939x, find the value of x.
Комментарии
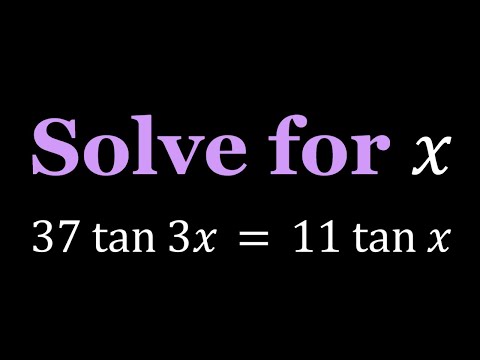 0:10:00
0:10:00
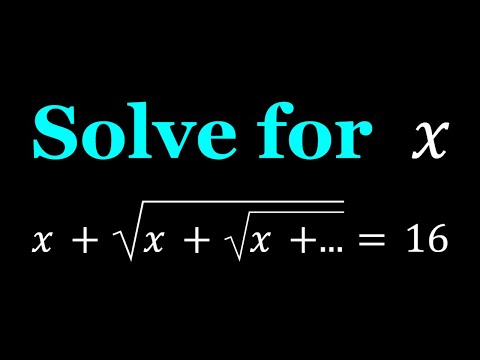 0:09:21
0:09:21
 0:01:36
0:01:36
 0:10:59
0:10:59
 0:11:57
0:11:57
 0:13:29
0:13:29
 0:10:40
0:10:40
 0:09:04
0:09:04
 0:09:36
0:09:36
 0:03:53
0:03:53
 0:08:33
0:08:33
 0:09:05
0:09:05
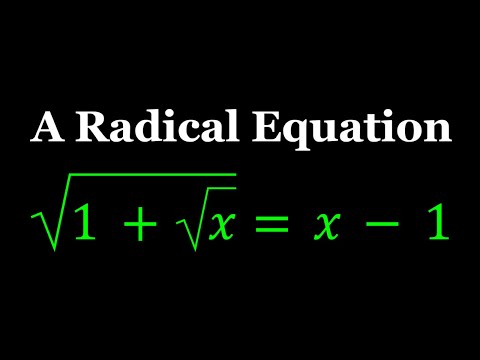 0:11:29
0:11:29
 0:11:49
0:11:49
 0:09:31
0:09:31
 0:12:37
0:12:37
 0:05:01
0:05:01
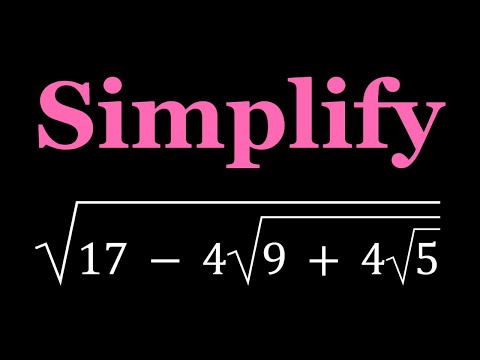 0:10:43
0:10:43
 0:08:14
0:08:14
 0:16:13
0:16:13
 0:12:46
0:12:46
 0:14:30
0:14:30
 0:08:42
0:08:42
 0:02:43
0:02:43