filmov
tv
Solving x^{1/sqrt(x)}=1/16
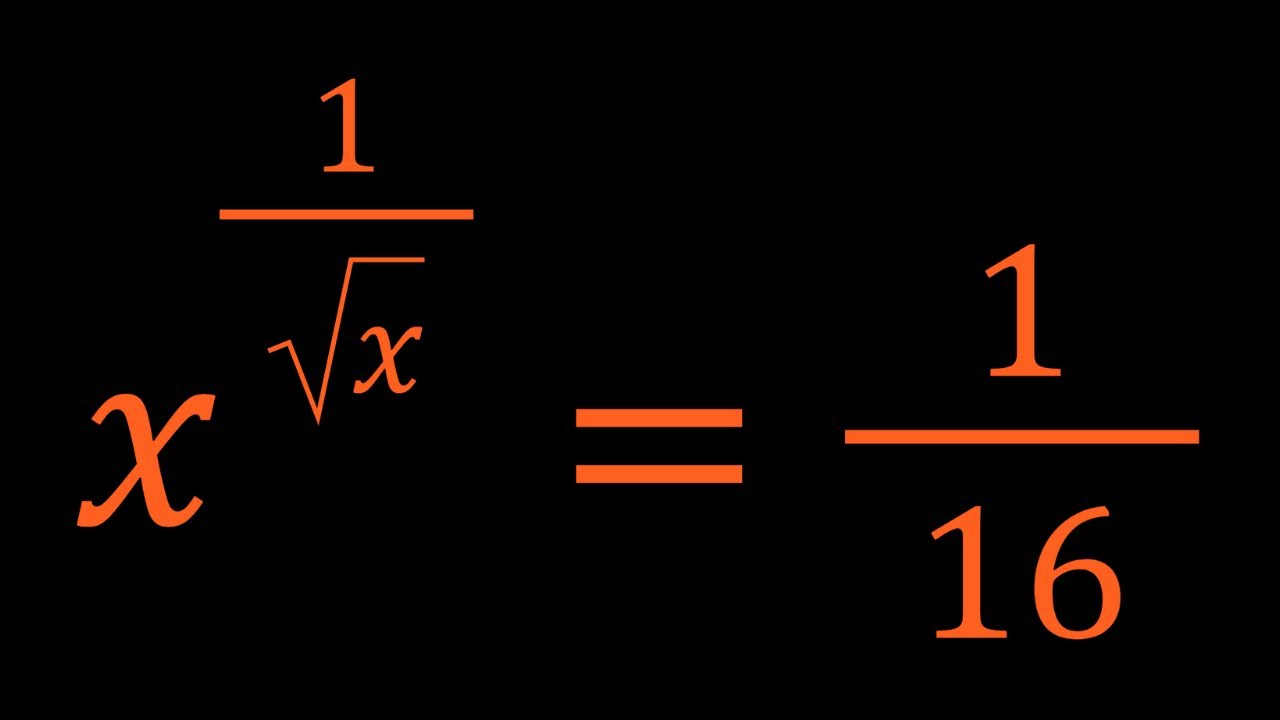
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Solving x^{1/sqrt(x)}=1/16
Solving x^2=-1 vs sqrt(x)=-1
Solve (x-1)/(sqrt x + 1) = 4 + (sqrt x - 1)/2
5 simple unsolvable equations
Solve Fast! | 16^x +16^x=1/4; Find x | Exponential Equations | Algebra Problems
Solving x^(-1+sqrt(2))x^(-1-sqrt(2))=16
Exponential Equations - Algebra and Precalculus
Human Calculator Solves World’s Longest Math Problem #shorts
Canada | Can You Solve? Math Olympiad Lectures |
Solving x^sqrt(x)=1/2, an Exponential Equation
How to solve this equation 4(x-1)=16 ...Watch for solution #equation #maths
Solve x-5=sqrt(x+1)
Solve an exponential equation by taking log of both sides & approximating the value
Solving sqrt(1+sqrt(x)) = x-1in Two Ways
X Grade : Quadratic Equations - Solve for x if sqrt((1-x)/x) + sqrt(x/(1-x)) = 13/6
Solve the equation sqrt(x+8) + sqrt(x+1) =7
Limit of (x - 1)/(sqrt(x + 3) - 2) as x approaches 1
Equations involving Indices
A Nice Exponential Equation (5^x-3^x=16)
Trying transition video for the first time 💙😂 || #transformation #transition #shorts #viralvideo...
Learn How to Solve a Square Root Equation
Fractions Butterfly Method #Short Video #Maths
Solve the equation `5^(x)root(x)(8^(x-1))=500`
Did you know this Fraction Tricks #math #mathematics #mathstricks #maths #mathhacks
Комментарии
 0:10:36
0:10:36
 0:00:58
0:00:58
 0:03:55
0:03:55
 0:00:50
0:00:50
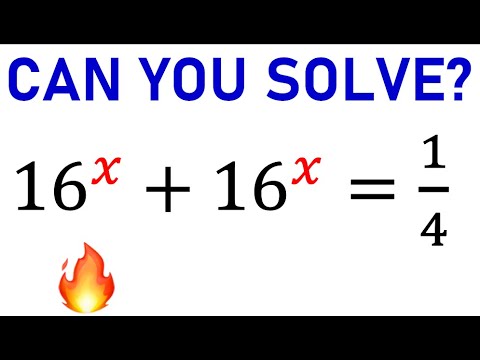 0:02:49
0:02:49
 0:01:29
0:01:29
 0:05:58
0:05:58
 0:00:34
0:00:34
 0:08:07
0:08:07
 0:09:57
0:09:57
 0:00:51
0:00:51
 0:04:21
0:04:21
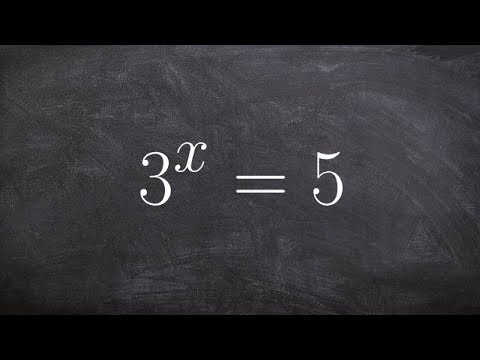 0:03:23
0:03:23
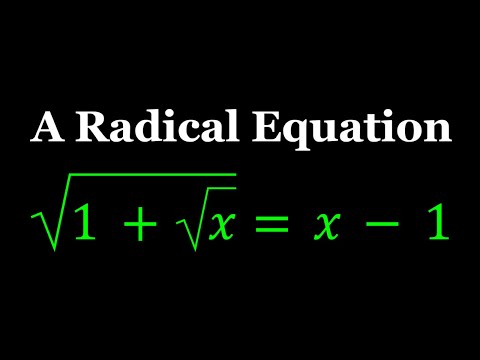 0:11:29
0:11:29
 0:04:06
0:04:06
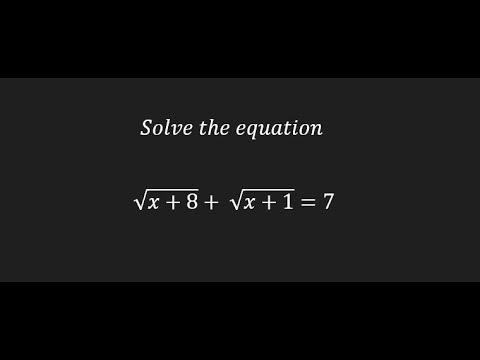 0:05:46
0:05:46
 0:02:08
0:02:08
 0:06:10
0:06:10
 0:06:37
0:06:37
 0:00:15
0:00:15
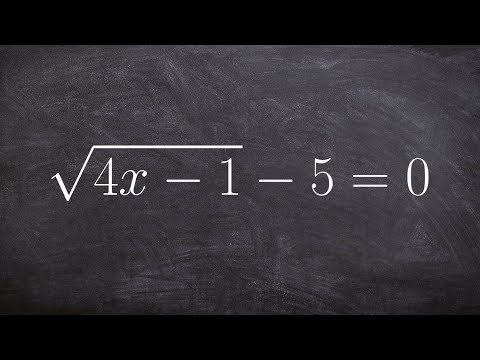 0:01:49
0:01:49
 0:00:27
0:00:27
 0:04:43
0:04:43
 0:01:00
0:01:00