filmov
tv
Black Scholes PDE Derivation using Delta Hedging

Показать описание
Explains the various approaches to derive the Black Scholes PDE using delta hedging and Ito's lemma
Black-Scholes PDE Derivation in 4 minutes
The Easiest Way to Derive the Black-Scholes Model
The Black Scholes PDE
Black Scholes PDE Derivation using Delta Hedging
Derivation of the Black-Scholes PDE
Introduction to the Black-Scholes formula | Finance & Capital Markets | Khan Academy
Transformation of Black Scholes PDE to Heat Equation
Derivation of Black-Scholes Equation |FULL|
The Math of 'The Trillion Dollar Equation'
Warren Buffett: Black-Scholes Formula Is Total Nonsense
Black Scholes Derivation from Heat Equation/ Diffusion Equation v2
Solving Black Scholes 1
The Trillion Dollar Equation
A simple derivation of the Black-Scholes equation
The Black-Scholes Model
Black-Scholes Equation (Financial Engineering)
Black Scholes Formula explained simply
Black Scholes Explained - A Mathematical Breakdown
Derivation of the Black-Scholes equation
Black Scholes Derivation
Introduction to Finite Difference Methods for Option Pricing
19. Black-Scholes Formula, Risk-neutral Valuation
Mastering the Black-Scholes Model: Essential Knowledge for Options Traders
1. Black Scholes - Deriving the PDE
Комментарии
 0:04:30
0:04:30
 0:09:53
0:09:53
 0:05:56
0:05:56
 0:12:45
0:12:45
 0:03:58
0:03:58
 0:10:24
0:10:24
 0:09:38
0:09:38
 0:00:12
0:00:12
 0:30:15
0:30:15
 0:15:54
0:15:54
 0:08:21
0:08:21
 0:48:36
0:48:36
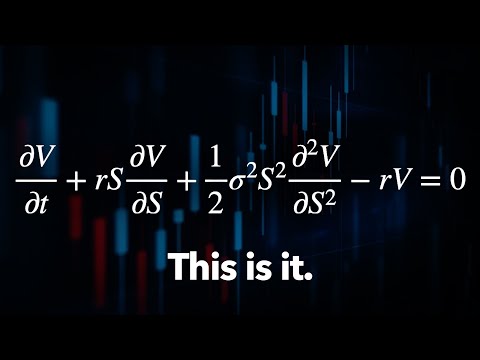 0:31:22
0:31:22
 0:27:31
0:27:31
 0:05:07
0:05:07
 0:05:59
0:05:59
 0:03:40
0:03:40
 0:14:03
0:14:03
 0:15:04
0:15:04
 0:16:55
0:16:55
 0:05:48
0:05:48
 0:49:52
0:49:52
 0:00:59
0:00:59
 0:38:44
0:38:44