filmov
tv
Linear Algebra 2j: Elements of ℝⁿ as Vectors - So Boring, yet so Important!

Показать описание
Linear Algebra 2j: Elements of ℝⁿ as Vectors - So Boring, yet so Important!
Linear combinations, span, and basis vectors | Chapter 2, Essence of linear algebra
Understanding Vector Spaces
Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra
Vectors | Chapter 1, Essence of linear algebra
Linear Algebra Example Problems - Linear Combination of Vectors #2
How to Prove a Set is a Subspace of a Vector Space
Linear Algebra - Matrix Operations
Rank and Nullity of Linear Transformations | Linear Algebra
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Linear Algebra Example Problems - Spanning Vectors #1
Gilbert Strang: Linear Algebra vs Calculus
Linear Algebra: Ch 2 - Determinants (22 of 48) The Cofactor of a Matrix
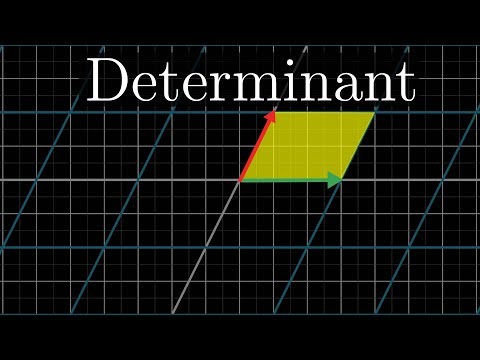
The determinant | Chapter 6, Essence of linear algebra
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
Linear Algebra 7 | Examples for Subspaces
Proof Based Linear Algebra Book
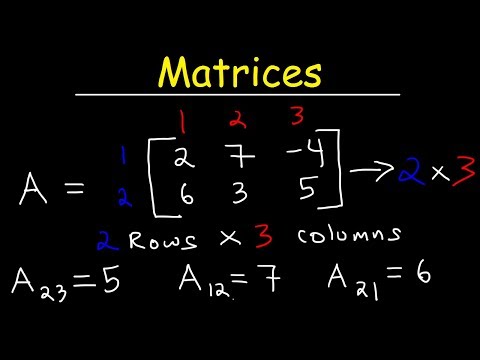
Intro to Matrices
Change of basis | Chapter 13, Essence of linear algebra
Linear Algebra - Lecture 28 - Subspaces
How to Find the Matrix of a Linear Transformation
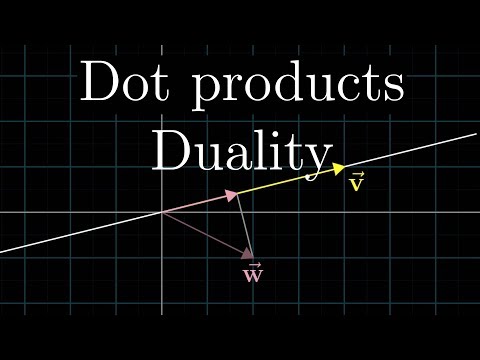
Dot products and duality | Chapter 9, Essence of linear algebra
Linear Algebra 2 - 1.5.5 - Basis for an Intersection or a Sum of two Subspaces (Video 2)
Linear Algebra Book With Solutions #mathematics #mathematics #maths
Комментарии
 0:09:03
0:09:03
 0:09:59
0:09:59
 0:08:41
0:08:41
 0:17:16
0:17:16
 0:09:52
0:09:52
 0:03:53
0:03:53
 0:05:58
0:05:58
 0:07:08
0:07:08
 0:09:05
0:09:05
 0:10:59
0:10:59
 0:04:31
0:04:31
 0:02:14
0:02:14
 0:04:13
0:04:13
 0:10:03
0:10:03
 0:13:52
0:13:52
 0:10:56
0:10:56
 0:00:24
0:00:24
 0:11:23
0:11:23
 0:12:51
0:12:51
 0:10:58
0:10:58
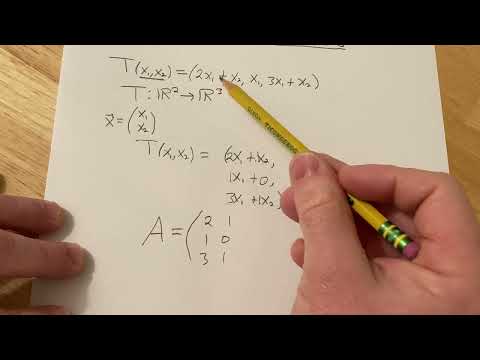 0:05:19
0:05:19
 0:14:12
0:14:12
 0:06:50
0:06:50
 0:00:59
0:00:59