filmov
tv
Linear Algebra - Lecture 28 - Subspaces

Показать описание
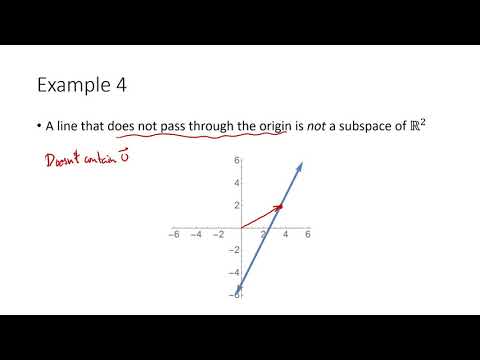
In this lecture, we define subspaces and view some examples and non-examples.
Linear Algebra - Lecture 28 - Subspaces
Linear Algebra - Lecture 28 - Null Space of a Matrix
Linear Algebra - Lecture 28 (modified) - Subspaces of R^n
Linear Algebra Lecture 28 | Orthogonal Vectors and Orthogonal Projection
Linear Algebra 28 | Conservation of Dimension
Operation Counts for Gaussian Elimination | Lecture 28 | Numerical Methods for Engineers
Linear Algebra 28 : Eigenvalues and Eigenvectors
NEWYES Calculator VS Casio calculator
Kernel and Range of Linear Transformations | Linear Algebra
Linear Algebra - Lecture 27: The Range and Null Space of a Matrix
Linear Algebra - Lecture 27 - Vector Spaces
Linear Algebra 28 | Conservation of Dimension [dark version]
Schaum's Outline for Linear Algebra 1968
#simplification #tricks
Lecture 28: Linear Algebra ( question based on direct sum of vector spaces )
Basis of a Vector Space | Examples | Linear Algebra | (Lecture 28) in Hindi
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Linear Algebra - Lecture 42: The Fibonacci Sequence via Diagonalization
Maths Ki Problem 😜 PIHOOZZ
Bro’s hacking life 😭🤣
Most Embarrassing Intro?! ft. Nikita Pawar | Ranveer Allahbadia Shorts
Linear Algebra: bilinear forms, metrics, geometry, music, 4-28-17
Algebra 28 - Solving Motion Problems with Linear Equations
Linear Algebra - Lecture 27 - Subspaces of R^n
Комментарии
 0:10:58
0:10:58
 0:13:03
0:13:03
 0:24:06
0:24:06
 0:23:09
0:23:09
 0:13:12
0:13:12
 0:09:00
0:09:00
 0:14:22
0:14:22
 0:00:14
0:00:14
 0:14:08
0:14:08
 0:13:49
0:13:49
 0:08:02
0:08:02
 0:13:14
0:13:14
 0:00:53
0:00:53
 0:00:11
0:00:11
 0:13:05
0:13:05
 0:12:09
0:12:09
 0:00:38
0:00:38
 0:13:16
0:13:16
 0:00:23
0:00:23
 0:00:20
0:00:20
 0:00:28
0:00:28
 0:54:10
0:54:10
 0:16:41
0:16:41
 0:24:55
0:24:55