filmov
tv
Linear Algebra 7 | Examples for Subspaces

Показать описание
Thanks to all supporters! They are mentioned in the credits of the video :)
This is my video series about Linear Algebra. I hope that it will help everyone who wants to learn about it.
#LinearAlgebra
#Vectors
#Matrices
#MachineLearning
#Eigenvalues
#Calculus
#Mathematics
x
(This explanation fits to lectures for students in their first year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
Linear Algebra 7 | Examples for Subspaces
Linear Algebra 7 | Examples for Subspaces [dark version]
Linear Algebra - Lecture 7 - Linear Combinations and Vector Equations
Linear Algebra Example Problems - Spanning Vectors #1
How to Solve Linear Equations With Variables on Both Sides : Linear Algebra Education
Linear Algebra Example Problems - Linear Combination of Vectors #2
Linear transformation examples: Rotations in R2 | Linear Algebra | Khan Academy
Solving Two-Step Equations | Expressions & Equations | Grade 7
General Linear Transformations on Vector Spaces | Linear Algebra
How to Find the Matrix of a Linear Transformation
❖ Using Gauss-Jordan to Solve a System of Three Linear Equations - Example 1 ❖
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
linear algebra vector space (25 examples)
Basic Algebra Tips
Vectors | Chapter 1, Essence of linear algebra
Linear Relationship Between Variables : Algebra
Number Theory | Linear Congruence Example 2
Gaussian Elimination & Row Echelon Form
Linear Equation | Solving Linear Equations
Algebra for Beginners | Basics of Algebra
Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra
Linear Algebra: Ch 2 - Determinants (13 of 48) Example of Rule 7: Transpose of a Matrix
How do we solve a system of linear equations using any method
Drawing Linear Graphs
Комментарии
 0:10:56
0:10:56
 0:10:58
0:10:58
 0:08:10
0:08:10
 0:04:31
0:04:31
 0:01:54
0:01:54
 0:03:53
0:03:53
 0:17:52
0:17:52
 0:03:40
0:03:40
 0:17:29
0:17:29
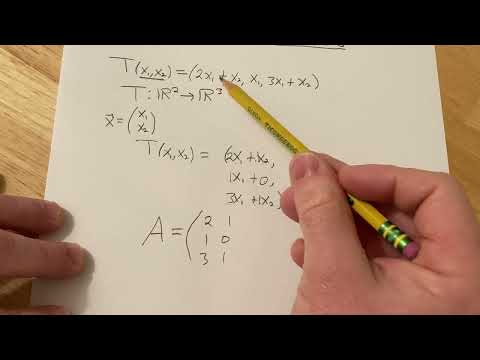 0:05:19
0:05:19
 0:07:12
0:07:12
 0:13:52
0:13:52
 0:30:16
0:30:16
 0:00:48
0:00:48
 0:09:52
0:09:52
 0:01:36
0:01:36
 0:04:44
0:04:44
 0:18:40
0:18:40
 0:11:20
0:11:20
 0:37:09
0:37:09
 0:12:09
0:12:09
 0:02:07
0:02:07
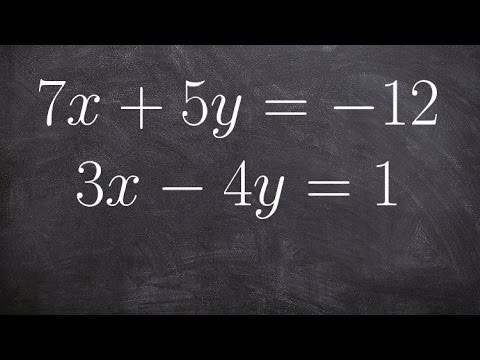 0:04:34
0:04:34
 0:05:57
0:05:57