filmov
tv
Solving 16^{x^2+y}+16^{x+y^2}=1
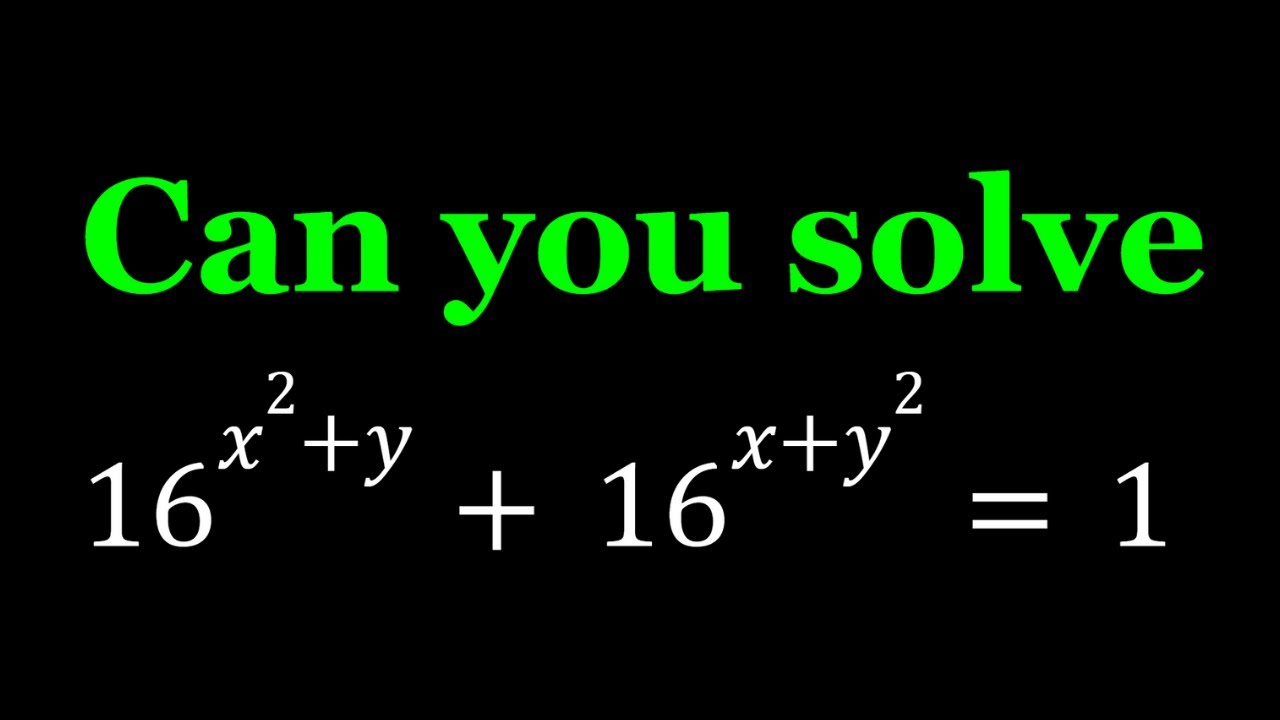
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #ExponentialEquations
PLAYLISTS 🎵 :
Solving 16^{x^2+y}+16^{x+y^2}=1
Solve the Nonlinear System of Equations 2x^2 - y^2 = 16, |x| = |y|
Exponential Equations - Algebra and Precalculus
Only 1 percent can solve this
Solving an equation for y and x
A Nice Exponential Equation (5^x-3^x=16)
Solving an equation for y and x using two steps
14.1 Domain and range for multi-variable functions
🔴PUNDITS SSC CGL LIVE MOCK 16 SOLUTION | SSC CGL PRE | TILL 18 AUG #ssccgl#ssc #ssccgl2024 #cgl2024...
Solving an equation with variables on both side and one solution
5 simple unsolvable equations
Second implicit derivative for x^2+y^2=16 using the chain rule and quotient rule
Trying transition video for the first time 💙😂 || #transformation #transition #shorts #viralvideo...
Method of Elimination Steps to Solve Simultaneous Equations
Graph a Circle: Write the Equation in Standard form 2x^2+2y^2+16x-12y+18=0
Simplify 16 x 2^(n+1) - 4 x 2^n / 16 x 2^(n+2) - 2 x 2^n+2. Simplify 16*2^n+1-4*2^n/16*2^n+2-2*2^n+2
Find the value of x and y
Sistema de Equações do 1º Grau (METÓDO DA ADIÇÃO).
Circle Diameter from equation: x² + y² = r² GCSE question
Writing an equation of circle tangent to the x axis given the center
Human Calculator Solves World’s Longest Math Problem #shorts
Solving x²-y²=5 for x,y greater than 0
Solve a system of equations with three variables
Determine whether an equation determines y as a functions of x
Комментарии
 0:08:35
0:08:35
 0:03:06
0:03:06
 0:05:58
0:05:58
 0:05:52
0:05:52
 0:03:47
0:03:47
 0:06:37
0:06:37
 0:03:12
0:03:12
 0:10:45
0:10:45
 1:09:45
1:09:45
 0:02:36
0:02:36
 0:00:50
0:00:50
 0:03:30
0:03:30
 0:00:15
0:00:15
 0:02:58
0:02:58
 0:06:05
0:06:05
 0:08:02
0:08:02
 0:04:55
0:04:55
 0:07:42
0:07:42
 0:00:59
0:00:59
 0:01:29
0:01:29
 0:00:34
0:00:34
 0:04:17
0:04:17
 0:09:00
0:09:00
 0:02:53
0:02:53