filmov
tv
Exponential Equations - Algebra and Precalculus
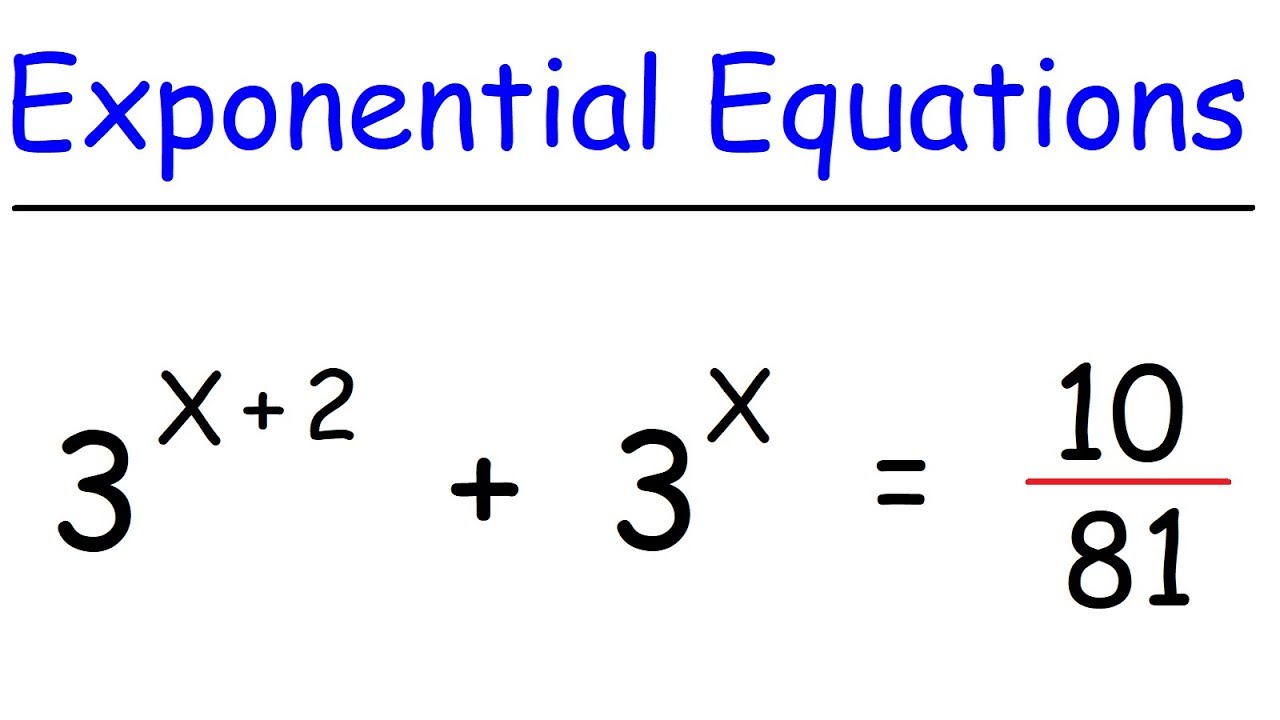
Показать описание
This Algebra and Precalculus video tutorial explains how to solve difficult exponential equations.
Log to Exponential Form:
Change of Base Formula:
Change of Base Log Problem:
Properties of Logarithms:
____________________________________
Expanding Logarithmic Expressions:
Condensing Logarithmic Expressions:
Natural Logarithms:
Solving Exponential Equations:
Exponential Equations - Quadratic Form:
_______________________________________
Solving Logarithmic Equations:
Graphing Logarithmic Functions:
Graphing Exponential Functions:
Compound Interest Word Problems:
Logarithms Practice Problems:
_______________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Log to Exponential Form:
Change of Base Formula:
Change of Base Log Problem:
Properties of Logarithms:
____________________________________
Expanding Logarithmic Expressions:
Condensing Logarithmic Expressions:
Natural Logarithms:
Solving Exponential Equations:
Exponential Equations - Quadratic Form:
_______________________________________
Solving Logarithmic Equations:
Graphing Logarithmic Functions:
Graphing Exponential Functions:
Compound Interest Word Problems:
Logarithms Practice Problems:
_______________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Exponential Equations - Algebra and Precalculus
Solving Exponential Equations
Exponential Equation Grade 10
Exponential growth functions | Exponential and logarithmic functions | Algebra II | Khan Academy
Exponential Equations – Algebra 2, Pre-Calculus, College Algebra
Solving an exponential equation with different bases
Exam Exponential Equations Grade 9
Simplifying Exponents With Fractions, Variables, Negative Exponents, Multiplication & Division, ...
Factorial Twist in an Exponential Equation! #shorts #math #short #exponents #algebra
Solving exponential equation | Exponential and logarithmic functions | Algebra II | Khan Academy
Grade 11 Equations Exam Questions | Exponential Equations
Introduction to Exponential Functions - Nerdstudy
Solving Exponential Equation
Solving Exponential and Logarithmic Equations
Can you solve this? | Exponential Equation | Algebra Problem.
How do I find x? Exponential equation with two different bases. Reddit precalculus r/Homworkhelp
Solving exponential equation with logarithm | Logarithms | Algebra II | Khan Academy
A Nice Math Olympiad Exponential Equation 3^x = X^9
Exponential Equations - College Algebra
Exponential Form to Logarithmic Form #Shorts #algebra #math #maths #mathematics #lesson #howto
Solving exponential equations using exponent properties | High School Math | Khan Academy
Evaluating and Graphing Exponential Functions
Solving Exponential Equation
how to solve an exponential equation with two different bases
Комментарии
 0:05:58
0:05:58
 0:16:36
0:16:36
 0:01:39
0:01:39
 0:07:41
0:07:41
 0:14:59
0:14:59
 0:03:01
0:03:01
 0:04:34
0:04:34
 0:11:48
0:11:48
 0:00:47
0:00:47
 0:05:12
0:05:12
 0:08:07
0:08:07
 0:03:22
0:03:22
 0:00:56
0:00:56
 0:07:08
0:07:08
 0:03:33
0:03:33
 0:07:47
0:07:47
 0:02:51
0:02:51
 0:02:34
0:02:34
 0:11:52
0:11:52
 0:00:22
0:00:22
 0:04:56
0:04:56
 0:05:59
0:05:59
 0:00:54
0:00:54
 0:03:21
0:03:21