filmov
tv
Second implicit derivative for x^2+y^2=16 using the chain rule and quotient rule
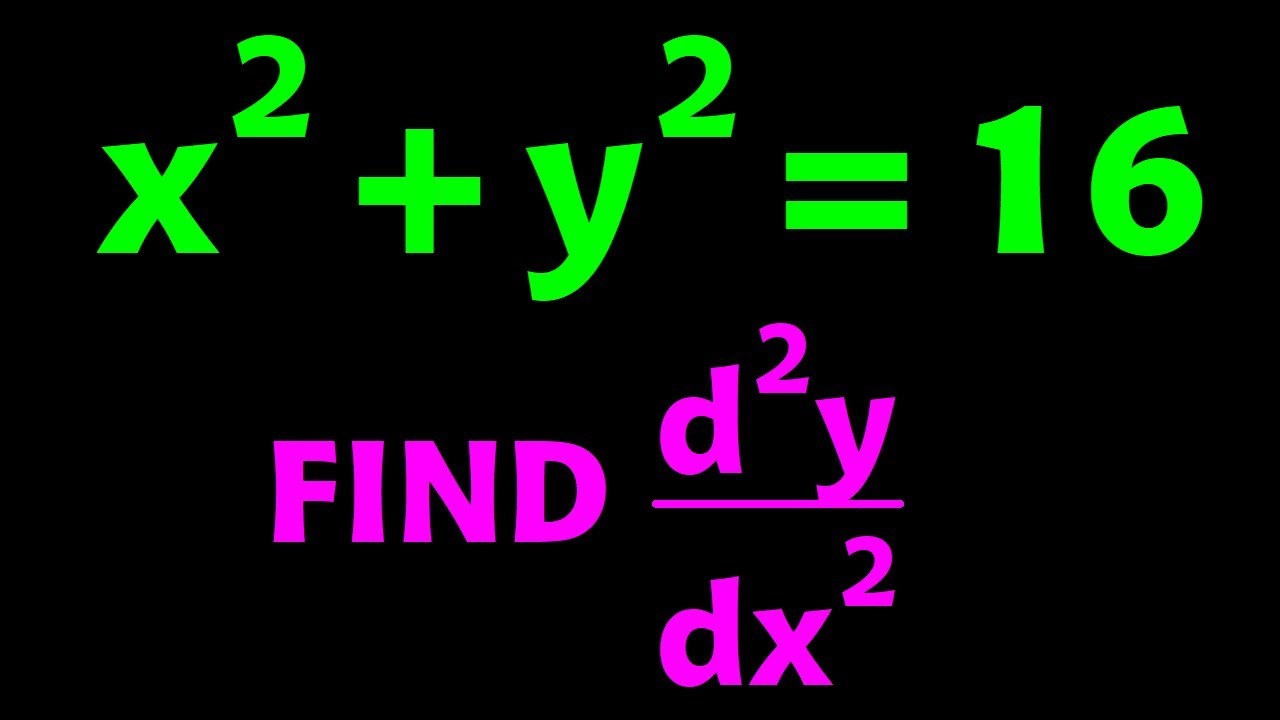
Показать описание
In this video, we will find the second derivative with respect to x of x squared plus y squared equals 16 using implicit differentiation. We must use the chain rule and quotient rule when differentiating this equation. To begin, we recognize that y really means y of x, which is some unknown function of x.
Differentiating x squared is simple, and we get 2x. To differentiate 2y, we bring the 2 down, multiply by y, and then multiply by the derivative of y, which is symbolically written as d y dx. On the right side of the equation, we have 16, which is a constant, and this derivative is 0.
We solve for d y dx by subtracting 2x from both sides, which gives us 2y d y dx = -2x. Dividing both sides by 2y, we cancel the 2y on the left side and get d y dx = -x/y, which is the first derivative.
To find the second derivative, we differentiate d y dx with respect to x and do the same thing on the right side. Since y is a function of x, we use the quotient rule to differentiate negative x over y. The quotient rule is low d high minus high d low over low squared.
We differentiate the bottom first, which is y. The derivative of the top is negative one, so we get d y dx times negative one. Subtracting that from the top, which is negative x, we get negative x minus y d 2y dx squared. This whole expression is then divided by y squared.
Combining like terms, we get negative y squared minus x squared over y squared divided by y squared. Factoring out a negative 1 from the top gives us negative 1 times y squared plus x squared over y squared divided by y squared.
Remembering that y squared minus x squared is equal to 16, we substitute and simplify to get negative 16 over y cubed. Therefore, the second derivative is negative 16 over y cubed.
In summary, we use implicit differentiation, the chain rule, and the quotient rule to find the second derivative with respect to x of x squared plus y squared equals 16. The first derivative is -x/y, and the second derivative is -16/y cubed.
🤔 Common Questions about Finding the Second Derivative 🤔
1. What is implicit differentiation?
Answer Implicit differentiation is a method of finding the derivative of a function that is not explicitly defined in terms of the independent variable.
2. What is the chain rule in calculus?
Answer The chain rule is a formula used to find the derivative of a composite function. It states that the derivative of f(g(x)) is equal to f'(g(x)) times g'(x).
3. What is the quotient rule in calculus?
Answer The quotient rule is a formula used to find the derivative of a quotient of two functions. It states that the derivative of f(x)/g(x) is equal to (g(x)f'(x) - f(x)g'(x))/g(x)^2.
4. What is the first derivative in calculus?
Answer The first derivative of a function is the rate of change of the function at a particular point. It is also known as the slope of the tangent line to the function at that point.
5. What is the second derivative in calculus?
Answer The second derivative of a function is the derivative of the first derivative. It describes the rate of change of the slope of the tangent line to the function at a particular point.
6. What is a constant function in calculus?
Answer A constant function is a function that always returns the same value regardless of the input. In
Differentiating x squared is simple, and we get 2x. To differentiate 2y, we bring the 2 down, multiply by y, and then multiply by the derivative of y, which is symbolically written as d y dx. On the right side of the equation, we have 16, which is a constant, and this derivative is 0.
We solve for d y dx by subtracting 2x from both sides, which gives us 2y d y dx = -2x. Dividing both sides by 2y, we cancel the 2y on the left side and get d y dx = -x/y, which is the first derivative.
To find the second derivative, we differentiate d y dx with respect to x and do the same thing on the right side. Since y is a function of x, we use the quotient rule to differentiate negative x over y. The quotient rule is low d high minus high d low over low squared.
We differentiate the bottom first, which is y. The derivative of the top is negative one, so we get d y dx times negative one. Subtracting that from the top, which is negative x, we get negative x minus y d 2y dx squared. This whole expression is then divided by y squared.
Combining like terms, we get negative y squared minus x squared over y squared divided by y squared. Factoring out a negative 1 from the top gives us negative 1 times y squared plus x squared over y squared divided by y squared.
Remembering that y squared minus x squared is equal to 16, we substitute and simplify to get negative 16 over y cubed. Therefore, the second derivative is negative 16 over y cubed.
In summary, we use implicit differentiation, the chain rule, and the quotient rule to find the second derivative with respect to x of x squared plus y squared equals 16. The first derivative is -x/y, and the second derivative is -16/y cubed.
🤔 Common Questions about Finding the Second Derivative 🤔
1. What is implicit differentiation?
Answer Implicit differentiation is a method of finding the derivative of a function that is not explicitly defined in terms of the independent variable.
2. What is the chain rule in calculus?
Answer The chain rule is a formula used to find the derivative of a composite function. It states that the derivative of f(g(x)) is equal to f'(g(x)) times g'(x).
3. What is the quotient rule in calculus?
Answer The quotient rule is a formula used to find the derivative of a quotient of two functions. It states that the derivative of f(x)/g(x) is equal to (g(x)f'(x) - f(x)g'(x))/g(x)^2.
4. What is the first derivative in calculus?
Answer The first derivative of a function is the rate of change of the function at a particular point. It is also known as the slope of the tangent line to the function at that point.
5. What is the second derivative in calculus?
Answer The second derivative of a function is the derivative of the first derivative. It describes the rate of change of the slope of the tangent line to the function at a particular point.
6. What is a constant function in calculus?
Answer A constant function is a function that always returns the same value regardless of the input. In
 0:03:30
0:03:30
 0:09:20
0:09:20
 0:03:41
0:03:41
 0:12:16
0:12:16
 0:05:13
0:05:13
 0:07:58
0:07:58
 0:04:29
0:04:29
 0:11:45
0:11:45
 0:08:46
0:08:46
 0:12:19
0:12:19
 0:05:23
0:05:23
 0:09:23
0:09:23
 0:06:46
0:06:46
 0:04:02
0:04:02
 0:03:08
0:03:08
 0:05:37
0:05:37
 0:07:16
0:07:16
 0:11:42
0:11:42
 0:10:38
0:10:38
 0:06:59
0:06:59
 0:08:29
0:08:29
 0:01:33
0:01:33
 0:03:34
0:03:34
 0:22:33
0:22:33