fx+y = fx + fy

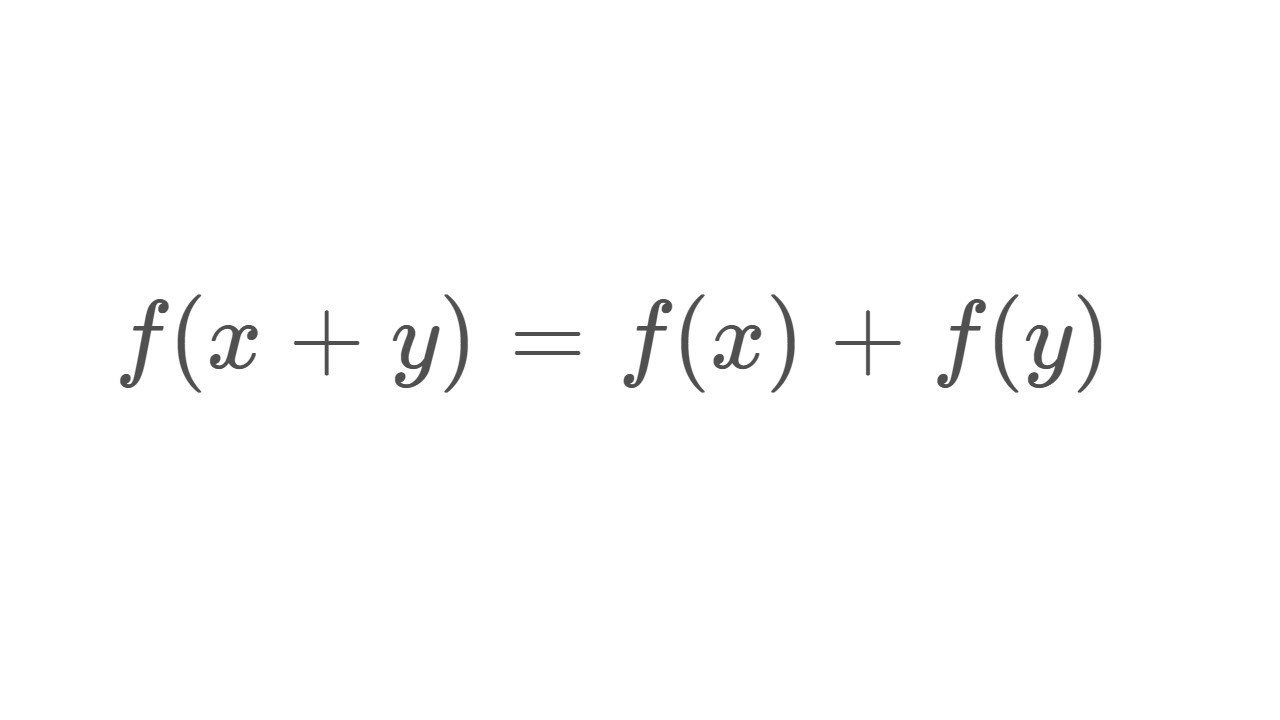
Показать описание

In this video, I find all functions f that satisfy f(x+y) = f(x) + f(y). Enjoy this amazing adventure through calculus, analysis, and linear algebra. Enjoy!

Рекомендации по теме

Комментарии

Everybody gangsta until peyam starts speaking spanish

giankk

As soon as the y changes to h it's like "OHH here come the derivatives" lol

I had this problem in a math competition a while ago and I used the f(m/n) = m/n f(1) method, but I never thought to use derivatives!

MuPrimeMath

When is a linear function not a linear function?
This video illustrates very nicely the two different meanings of the term linear function in Maths. Your final f is not linear in a functions sense but is linear in a linear algebra sense.
After a few moments of thinking about this problem I realised that without the assumption of continuity, one has to think of R as a vector space over Q, and then f can be any linear function (mapping R to R as vector spaces over Q). You can then choose any basis for R over Q (with a bit of help from the axiom of choice) and then assign any values to f on each basis element. This is essentially what you said, but I don't think you mentioned the axiom of choice.

MichaelRothwell

I was hoping that you'll also talk about functions with discrete domain. for example, defined over natural numbers.

rshell

Just in synch with Socratica coming back to her Group Theory series with an episode on Homomorphisms.

Icenri

In measure theory we showed that the image of any interval [a, b], a, b element R under an additive, but not linear function f is not bounded.
Which blew my mind

Leidl.Michael

I always wondered why linearity was defined with both conditions! Thanks!

mathijsj

Excellent class Dr Peyam! I love your videos! Cheers from Brazil

mundodejoel

Beware of the anti-axiom of choice crowd. They don't take kindly to these sorts of shenanigans.

michaelz

A ha! You've assumed that all vector spaces indeed *have* a basis! Very sneaky. Just kidding; pretty much everybody now accepts the Axiom of Choice. It's just too tempting to bring it up whenever it's used.

alexandersanchez

A ques appeared in my exam just days ago based on additive functions and I solved it just because I've seen this video

I'm here again to thank you !

vibhav

This "Cauchy's equation" showed up in the IMO qualifier I was in... good old time.
I found the general solution by claiming there is a set of "basic" irrational numbers. Thus the word "basis" makes perfect sense to me.
Well I wasn't able to explain my answer LOL. Maybe that's how I got kicked out.

shinli

I found it really useful, thank you so much for making this videos

unaicanudas

This almost feels like it’s leading to the concept of impulse functions and convolutions. A very important concept in signal processing.

tylershepard

Was very profound! If you multiply the Dirichlet-function with x you get also a function that is linear on both: rational and irrational numbers, but that is not linear on the real numbers.

WerIstWieJesus

12:00 we could have taken 1 instead of √2
So the function is 0 on irrational numbers and Cx on rationals

rubengirona

I really.... liked Galois Theory. Nice Video, greetings from Germany

aik

You remind me of a guy I asked to work with. Except you're a dr. And good at math lol

Varde

Thanks a lot for making these videos, I'm currently studying for a test and this video helped me out a lot

nathantrance

Great work! 😀
Now solve the equation in the most general case, f is a function from V to W where V and W are vector spaces. 😁

YouTube_username_not_found

fx+y = fx + fy

fx+y = fx + fy

Solving the Functional Equation f(x+y)=f(x)f(y)

Find the partial derivatives, fx and fy, for f(x,y)=8x^{2}-6xy^{2}+3y+21 | Plainmath

f(x+y) = f(x)f(y)

VECTORES VIDEO 2. COMPONENTES Fx y Fy y VECTOR RESULTANTE

Derivadas parciales de f(x,y)=√xLny | Derivadas fx, fy, fxx, fyy, fxy, fyx | La Prof Lina M3

Calculus 3 Assignment #3 -- Partial Derivatives : fx, fy, fxx, fyy, fxy, fyx

Partial Derivatives - Multivariable Calculus

Probability Distributions | Random Variables | Continuous Random Variables | Graph of the CDF | 44 |

Derivadas parciales fx(x,y) y fy(x,y) | La Prof Lina M3

Primera y segunda derivada parcial (fx, fy, fxx, fyy)

Connecting f, f', and f'' graphically | AP Calculus AB | Khan Academy

Difference Between Partial and Total Derivative

analyse synthèse fxfy fxy prépa MPSI postbac

Learn how to evaluate for a function

How to find Partial Derivative of a function

If fx+y,x&minus;y=xy, then&nbsp;fx,y+fy,x2=....

Calculus 3: Partial Derivative (14 of 30) Find More Partial Derivatives: Example (2 of 2)

analyse synthèse fx fy prépa MPSI postbac

First order derivative |find fx and fy

Evaluar Fx y Fy en el punto dado (arcoseno)

Geometric Interpretation of Fx and Fy in Partial derivatives

Total Differential of Multivariate Function f(x, y) = x^3y^4 + x^2y^3 + 12

Easily solve Maximum & Minimum values of the function good example(PART-1)

If fx+y,x−y=xy, then fx,y+fy,x2=....