ODE | Phase diagrams

Показать описание

Examples and explanations for a course in ordinary differential equations.

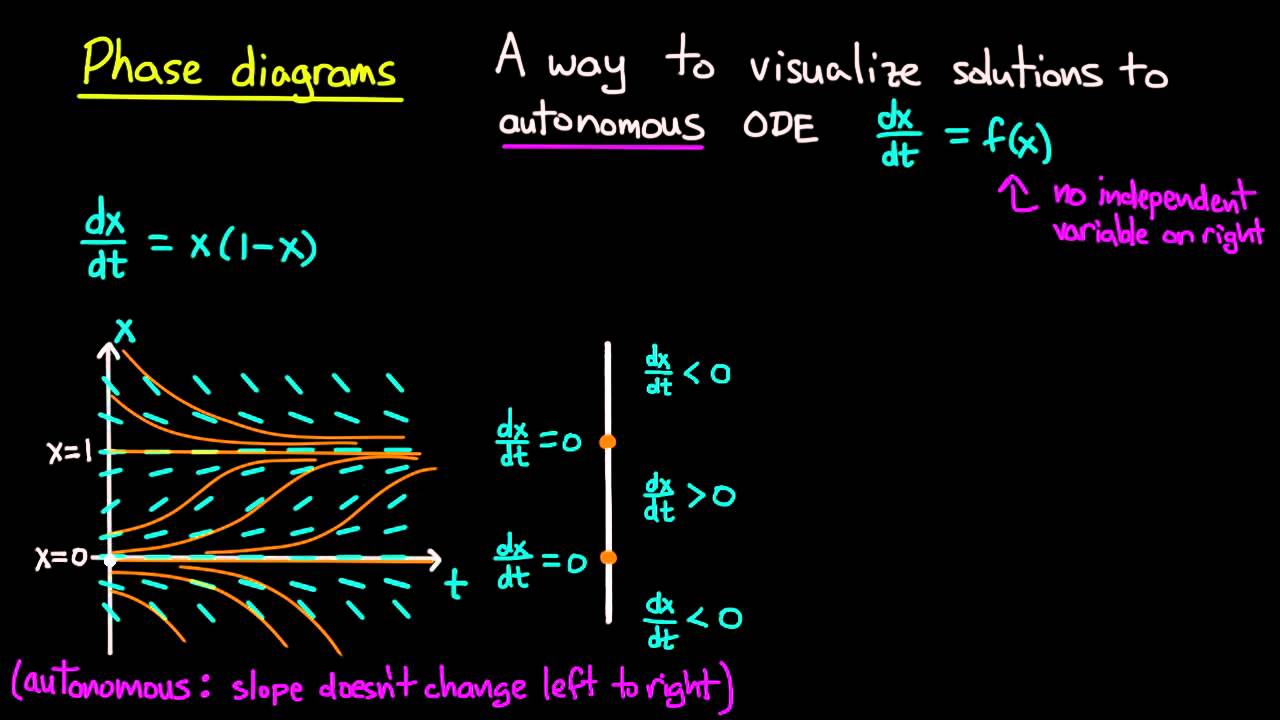
In this video we explain how to construct a phase diagram (or phase portrait) for an autonomous first order differential equation using the example of the logistic equation. With one dependent variable, our phase diagram is a phase line. We also give examples of stable and unstable equilibrium points.

Рекомендации по теме

Комментарии

I rarely comment on these videos but this 5 minute video, most of which I skimmed through, explained more than I'll ever learn reading the corresponding chapter in this piece of crap 200 dollar textbook. Thanks for the videos man.

b-rog

Felt so lost in my differential equations class, but not anymore! really clear and helpful!

Thegoshjosh

I dont typically comment on videos but this video explained more to me than a 1 hour lecture and a full chapter in my textbook, and it did it in 5 minutes. Thank you so much and i hope to see more videos!

wyatt

I was reading a research paper in Controls Theory which talked about phase diagrams, and I had no idea of what it was. I'm aghast at how a 5 minutes video was able to teach me it! Excellent video!

kabascoolr

Hello sir, your voice is heavenly and your explanation is Godly. Thank you so much. This is possibly the best explanation I have seen so far.

TheAInfinity

You are simply I have an ODE exam this Friday and I am going over all you videos and this is helping me a lot! Thank you!!

ElemenT

I don't understand why uni's don't just hire guys like you to make content like this for their courses. Why do millions of people each year have to sit through incomprehensible multi hour long lectures and then come to youtube for better understanding in 5 mins, it blows my mind.

Zoonofski

Differential equations is so confusing, but once I get a grasp of what’s going on, it’s really cool to see how we could examine solution curves without even touching the DE

MrBryanjaziel

This video needs more views. Lifesaver before my first exam.

jarjarrose

saving grades on a daily basis, thanks man

flurizer

I believe the answer to the first challenge is have a point of inflection - thus cubic (in x) 'dx/dt'.

There's a time symmetry in the slope field, I noticed, so 'unstable' and 'stable' solutions are precisely dual w.r.t which way the film runs in the projector. This does suggest we can have stable inflections as easily as unstable ones - and thus have the 'full set'.

Are you intending to do any 'numerical' (iterative) methods of solution in this course I wonder?

pauluk

Your explanations and videos are great quality, and easy to follow. That is why you need to make more videos!

vusiliyK

Thanks. Nice Simple, Clear Video, Clear Audio. Your legibility sense is good. Thanks for eliminating thin hairlines which are difficult to see. You get the videofountain .. Clarity Award for September 2013.

videofountain