filmov
tv
Solving a quintic equation with a non-standard method. An algebraic challenge.
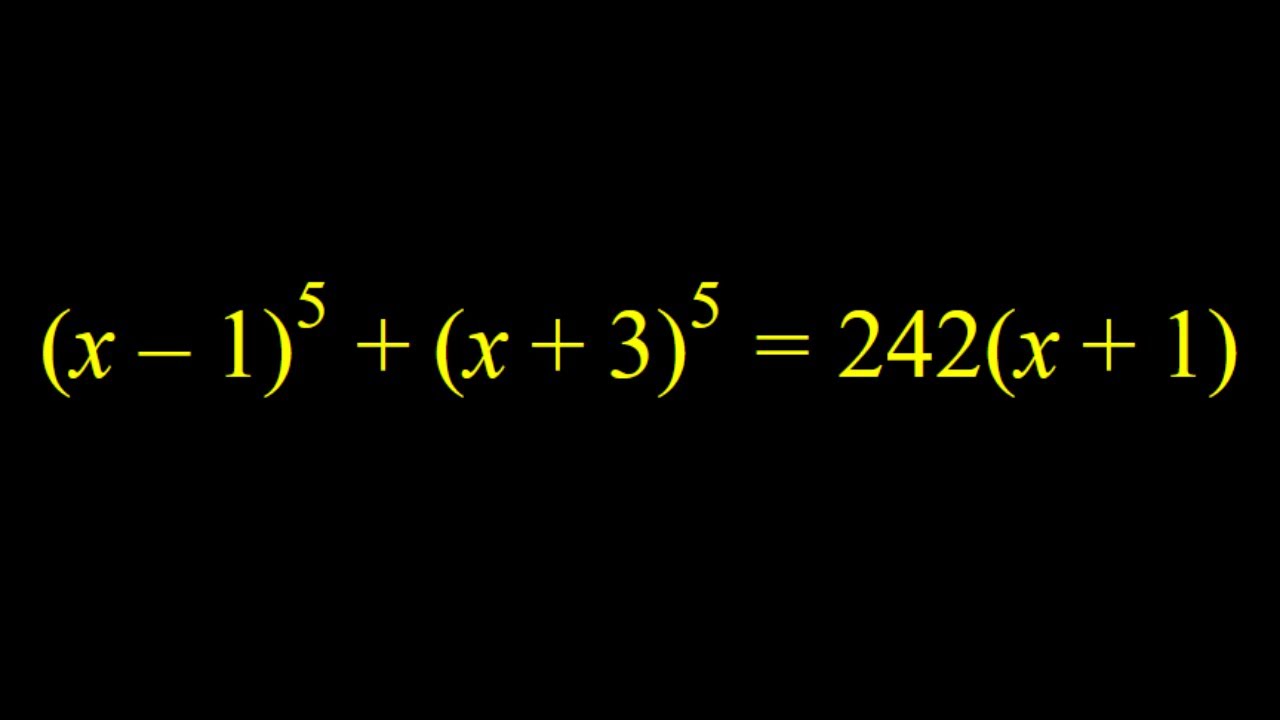
Показать описание
This video is about a quintic equation that can be solved by using algebraic tricks.
Polynomial expressions, algebra, algebraic equations, SyberMath, algebraic manipulations, equations, substitution, Challenging Math Problems, Non-routine Math Problems, Polynomial equations, an algebraic challenge, algebraic identities, an equation,, non-standard methods, quintic equations
Polynomial expressions, algebra, algebraic equations, SyberMath, algebraic manipulations, equations, substitution, Challenging Math Problems, Non-routine Math Problems, Polynomial equations, an algebraic challenge, algebraic identities, an equation,, non-standard methods, quintic equations
I can solve any quintic equation!!
EXTREME quintic equation! (very tiring)
Why There's 'No' Quintic Formula (proof without Galois theory)
Solving A Quintic | Polynomial Equations #maths
Why you can't solve quintic equations (Galois theory approach) #SoME2
solving equations but they get increasingly awesome
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
Solving a Quintic Equation
solving a 6-term quintic equation
My First Quintic Equation
An Overview of the True Quintic Formula...and Why You Should Never Use It
But why is there no quintic formula? | Galois Theory
so you want to see the cubic formula
Solving a quintic equation with a non-standard method. An algebraic challenge.
Solving the Quintic Equation z^5 + 32 = 0 - Complex Analysis
Can you solve the Quintic Equation for x? | Olympiad Mathematics | Math Olympiad Training
Solving a simple cubic equation. A trick you should know!
de Moivre quintic formula
How To Solve A Quintic Equation | Algebra | Math Olympiad
Algebra 10: Solving Real Root of Quintic Equation in FASTER Way
Numerical solution of quintic equations using bootstrapping | Solving Poly Eqns 38 | Wild Egg Maths
Solution for a particular general quintic equation
Quintic Equation From Chebyshev Polynomial
How to Solve this Quintic Polynomial Related Problem?
Комментарии
 0:22:51
0:22:51
 0:31:27
0:31:27
 0:45:04
0:45:04
 0:03:58
0:03:58
 0:45:24
0:45:24
 0:10:44
0:10:44
 0:36:58
0:36:58
 0:08:44
0:08:44
 0:04:24
0:04:24
 0:10:29
0:10:29
 0:35:21
0:35:21
 0:11:59
0:11:59
 0:40:16
0:40:16
 0:09:49
0:09:49
 0:04:17
0:04:17
 0:05:54
0:05:54
 0:06:41
0:06:41
 0:29:02
0:29:02
 0:10:42
0:10:42
 0:04:55
0:04:55
 0:22:49
0:22:49
 0:02:37
0:02:37
 0:22:20
0:22:20
 0:04:43
0:04:43