filmov
tv
I can solve any quintic equation!!

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
I can solve any quintic equation!!
Why you can't solve quintic equations (Galois theory approach) #SoME2
Why There's 'No' Quintic Formula (proof without Galois theory)
The Insolvability of the Quintic
But why is there no quintic formula? | Galois Theory
solving equations but they get increasingly awesome
5 simple unsolvable equations
An Overview of the True Quintic Formula...and Why You Should Never Use It
AP Calculus AB 5.5 Find the Inflection Points of a Quintic Function
An Interesting Golden Quintic Equation
EXTREME quintic equation! (very tiring)
Grant Sanderson (3Blue1Brown) | Unsolvability of the Quintic | The Cartesian Cafe w/ Timothy Nguyen
Can you solve the Quintic Equation for x? | Olympiad Mathematics | Math Olympiad Training
Solving a QUINTIC Equation | Without CALCULATOR | Deconstructive Polynomial Factorization
How REAL Men Integrate Functions
Can You Factories A Quintic Trinomial in Just 40 Seconds? | #Shorts
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
Can We Solve A Quintic
Quintic Equation
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Cracking the Quintic Equation Code: Two Techniques for Solving with Ease
How to Solve this Quintic Polynomial Related Problem?
SOLVING QUINTIC EQUATION x^5 = x^2 | find all real x #igcse #math #maths
Algebra 10: Solving Real Root of Quintic Equation in FASTER Way
Комментарии
 0:22:51
0:22:51
 0:45:24
0:45:24
 0:45:04
0:45:04
 0:10:19
0:10:19
 0:11:59
0:11:59
 0:10:44
0:10:44
 0:00:50
0:00:50
 0:35:21
0:35:21
 0:03:00
0:03:00
 0:05:50
0:05:50
 0:31:27
0:31:27
 2:19:34
2:19:34
 0:05:54
0:05:54
 0:24:59
0:24:59
 0:00:35
0:00:35
 0:00:55
0:00:55
 0:36:58
0:36:58
 0:08:14
0:08:14
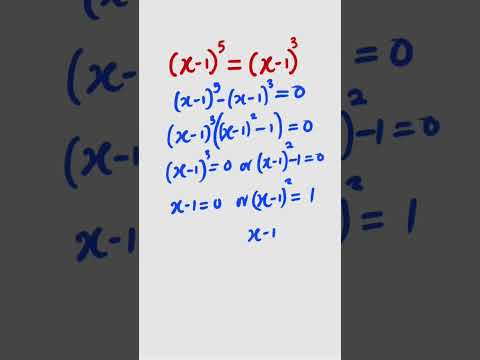 0:00:58
0:00:58
 0:00:38
0:00:38
 0:20:29
0:20:29
 0:04:43
0:04:43
 0:00:59
0:00:59
 0:04:55
0:04:55