filmov
tv
Why you can't solve quintic equations (Galois theory approach) #SoME2

Показать описание
An entry to #SoME2. It is a famous theorem (called Abel-Ruffini theorem) that there is no quintic formula, or quintic equations are not solvable; but very likely you are not told the exact reason why. Here is how traditionally we knew that such a formula cannot exist, using Galois theory.
Correction: At 08:09, I forgot to put ellipsis in between.
Video chapters:
00:00 Introduction
00:23 Chapter 1: The setup
04:38 Chapter 2: Galois group
11:15 Chapter 3: Cyclotomic and Kummer extensions
19:43 Chapter 4: Tower of extensions
27:25 Chapter 5: Back to solving equations
35:23 Chapter 6: The final stretch (intuition)
43:25 Chapter 7: What have we done?
Notes:
I HAVE to simplify and not give every technical detail. This is made with the intent that everyone, regardless of their background in algebra, can take away the core message of the video. This can only be done if I cut out the parts that are not necessary for this purpose. As with my previous video series on “Average distance in a unit disc”, this is made to address the question I always had when I was small - treat this as a kind of a video message to my past self.
The reason we have this mess is that we defined Galois extension using the splitting field of a (separable, i.e. no repeated roots) polynomial. The usual definition given is exactly as above - only things fixed by ALL automorphisms over Q must be in Q itself. This typical definition will of course solve the problem above, but will now create the problem of why this definition implies the larger field is made by adjoining the roots of some polynomial. These two definitions are equivalent, but I just think that it makes much more sense to define it the way I did in the video, in the context of the video; and also I think this is an easier definition to accept.
[The question is already the proof - it is a really elementary way to show the result that we want]
More resources on proofs that A_n is not solvable:
[You need to only go up to Page 5 towards the end of the proof of Theorem 2, but you definitely need group theory lingo]
Other than commenting on the video, you are very welcome to fill in a Google form linked below, which helps me make better videos by catering for your math levels:
If you want to know more interesting Mathematics, stay tuned for the next video!
SUBSCRIBE and see you in the next video!
If you are wondering how I made all these videos, even though it is stylistically similar to 3Blue1Brown, I don't use his animation engine Manim, but I will probably reveal how I did it in a potential subscriber milestone, so do subscribe!
Social media:
For my contact email, check my About page on a PC.
See you next time!
Correction: At 08:09, I forgot to put ellipsis in between.
Video chapters:
00:00 Introduction
00:23 Chapter 1: The setup
04:38 Chapter 2: Galois group
11:15 Chapter 3: Cyclotomic and Kummer extensions
19:43 Chapter 4: Tower of extensions
27:25 Chapter 5: Back to solving equations
35:23 Chapter 6: The final stretch (intuition)
43:25 Chapter 7: What have we done?
Notes:
I HAVE to simplify and not give every technical detail. This is made with the intent that everyone, regardless of their background in algebra, can take away the core message of the video. This can only be done if I cut out the parts that are not necessary for this purpose. As with my previous video series on “Average distance in a unit disc”, this is made to address the question I always had when I was small - treat this as a kind of a video message to my past self.
The reason we have this mess is that we defined Galois extension using the splitting field of a (separable, i.e. no repeated roots) polynomial. The usual definition given is exactly as above - only things fixed by ALL automorphisms over Q must be in Q itself. This typical definition will of course solve the problem above, but will now create the problem of why this definition implies the larger field is made by adjoining the roots of some polynomial. These two definitions are equivalent, but I just think that it makes much more sense to define it the way I did in the video, in the context of the video; and also I think this is an easier definition to accept.
[The question is already the proof - it is a really elementary way to show the result that we want]
More resources on proofs that A_n is not solvable:
[You need to only go up to Page 5 towards the end of the proof of Theorem 2, but you definitely need group theory lingo]
Other than commenting on the video, you are very welcome to fill in a Google form linked below, which helps me make better videos by catering for your math levels:
If you want to know more interesting Mathematics, stay tuned for the next video!
SUBSCRIBE and see you in the next video!
If you are wondering how I made all these videos, even though it is stylistically similar to 3Blue1Brown, I don't use his animation engine Manim, but I will probably reveal how I did it in a potential subscriber milestone, so do subscribe!
Social media:
For my contact email, check my About page on a PC.
See you next time!
Комментарии
 0:45:24
0:45:24
 0:45:04
0:45:04
 0:11:59
0:11:59
 0:10:19
0:10:19
 0:35:21
0:35:21
 0:22:51
0:22:51
 0:00:38
0:00:38
 0:36:58
0:36:58
 2:19:34
2:19:34
 0:00:50
0:00:50
 0:10:44
0:10:44
 0:10:04
0:10:04
 0:29:02
0:29:02
 0:31:27
0:31:27
 0:05:54
0:05:54
 0:08:14
0:08:14
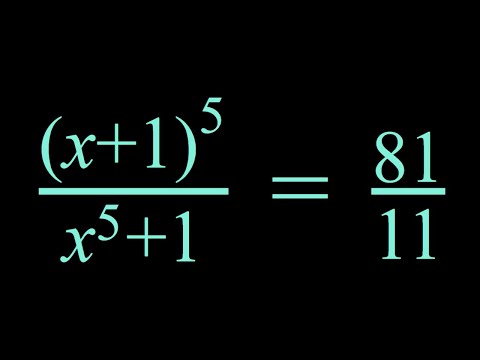 0:14:01
0:14:01
 0:00:56
0:00:56
 0:04:43
0:04:43
 0:17:00
0:17:00
 0:08:12
0:08:12
 1:13:55
1:13:55
 0:06:38
0:06:38
 0:00:35
0:00:35