filmov
tv
Why There's 'No' Quintic Formula (proof without Galois theory)

Показать описание
Feel free to skip to 10:28 to see how to develop Vladimir Arnold's amazingly beautiful argument for the non-existence of a general algebraic formula for solving quintic equations! This result, known as the Abel-Ruffini theorem, is usually proved by Galois theory, which is hard and not very intuitive. But this approach uses little more than some basic properties of complex numbers. (PS: I forgot to mention Abel's original approach, which is a bit grim, and gives very little intuition at all!)
00:00 Introduction
01:58 Complex Number Refresher
04:11 Fundamental Theorem of Algebra (Proof)
10:28 The Symmetry of Solutions to Polynomials
22:47 Why Roots Aren't Enough
28:29 Why Nested Roots Aren't Enough
37:01 Onto The Quintic
41:03 Conclusion
00:00 Introduction
01:58 Complex Number Refresher
04:11 Fundamental Theorem of Algebra (Proof)
10:28 The Symmetry of Solutions to Polynomials
22:47 Why Roots Aren't Enough
28:29 Why Nested Roots Aren't Enough
37:01 Onto The Quintic
41:03 Conclusion
Why There's 'No' Quintic Formula (proof without Galois theory)
But why is there no quintic formula? | Galois Theory
Why you can't solve quintic equations (Galois theory approach) #SoME2
The Insolvability of the Quintic
Grant Sanderson (3Blue1Brown) | Unsolvability of the Quintic | The Cartesian Cafe w/ Timothy Nguyen
5 simple unsolvable equations
When mathematicians get bored (ep1)
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Non-Existence of the Quintic Formula
solving equations but they get increasingly awesome
why calculus students struggle
de Moivre quintic formula
How do we know the quintic is unsolvable?
An Overview of the True Quintic Formula...and Why You Should Never Use It
How REAL Men Integrate Functions
EXTREME quintic equation! (very tiring)
How Imaginary Numbers Were Invented
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
What is...the Abel-Ruffini theorem?
I can solve any quintic equation!!
A Quintic Equation Solved Without The Quintic Formula
Is there a formula for primes ? (Spoiler: YES and NO)
Abel’s and Galois’s Proofs on Quintic Equations having no Radical Solutions are Invalid
Abel's Impossibility Theorem
Комментарии
 0:45:04
0:45:04
 0:11:59
0:11:59
 0:45:24
0:45:24
 0:10:19
0:10:19
 2:19:34
2:19:34
 0:00:50
0:00:50
 0:00:37
0:00:37
 0:00:38
0:00:38
 0:57:32
0:57:32
 0:10:44
0:10:44
 0:00:09
0:00:09
 0:29:02
0:29:02
 0:55:59
0:55:59
 0:35:21
0:35:21
 0:00:35
0:00:35
 0:31:27
0:31:27
 0:23:29
0:23:29
 0:36:58
0:36:58
 0:32:44
0:32:44
 0:22:51
0:22:51
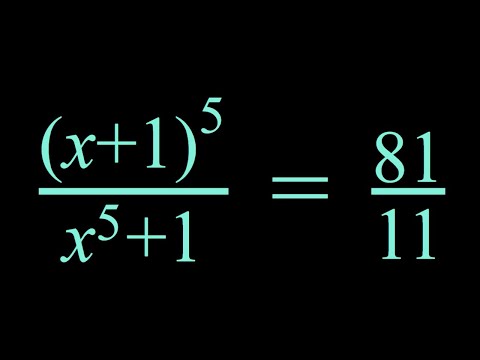 0:14:01
0:14:01
 0:05:40
0:05:40
 0:03:25
0:03:25
 0:03:08
0:03:08