filmov
tv
Numerical solution of quintic equations using bootstrapping | Solving Poly Eqns 38 | Wild Egg Maths
Показать описание
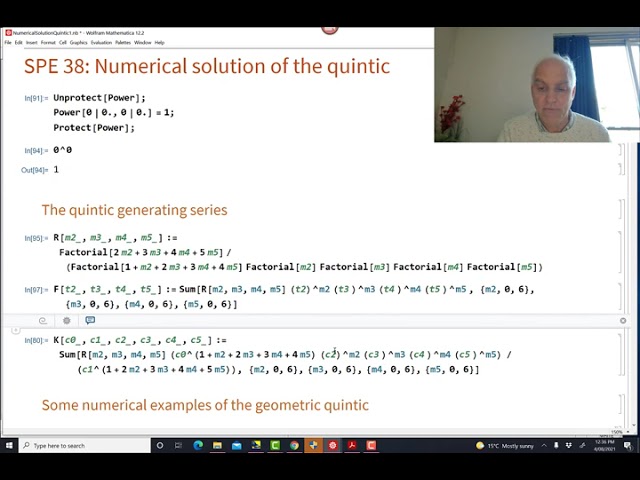
The problem of solving quintic equations has generated considerable interest over the centuries. From the point of view of Galois theory, it is generally thought that solutions of such equations are intrinsically different from lower degree equations, at least in terms of finding formulas using expressions with radicals.
In particular, theoretical procedures for generating even approximate solutions using numerical methods are not known, or at least not widely known.
However in this series Solving Polynomial Equations, we have developed a powerful new algebraic way of solving general equations using a massive generalization of the Catalan story, involving roofed subdivided polygons (RSP's) and associated power series as suitable generating functions. Let's now see if we can use this novel technology to get approximate numerical solutions to explicit quintic equations!
The method of bootstrapping will be particularly useful here; this is a procedure outlined in the previous videos for using approximated solutions to generate more accurate ones. We will be happily harnessing the power of Wolfram Mathematica to help us!
The ideas here generate a wide range of questions and additional avenues for exploration -- this is fertile ground for keen amateur explorers of mathematics, and fits nicely into our general plan of laying our fruitful directions to Explore Research Level Mathematics.
************************
Here are the Wild Egg Maths Playlists (some available only to Members!)
***********************
Here are the Insights into Mathematics Playlists:
list=PL8403C2F0C89B1333
In particular, theoretical procedures for generating even approximate solutions using numerical methods are not known, or at least not widely known.
However in this series Solving Polynomial Equations, we have developed a powerful new algebraic way of solving general equations using a massive generalization of the Catalan story, involving roofed subdivided polygons (RSP's) and associated power series as suitable generating functions. Let's now see if we can use this novel technology to get approximate numerical solutions to explicit quintic equations!
The method of bootstrapping will be particularly useful here; this is a procedure outlined in the previous videos for using approximated solutions to generate more accurate ones. We will be happily harnessing the power of Wolfram Mathematica to help us!
The ideas here generate a wide range of questions and additional avenues for exploration -- this is fertile ground for keen amateur explorers of mathematics, and fits nicely into our general plan of laying our fruitful directions to Explore Research Level Mathematics.
************************
Here are the Wild Egg Maths Playlists (some available only to Members!)
***********************
Here are the Insights into Mathematics Playlists:
list=PL8403C2F0C89B1333
Комментарии
 0:22:49
0:22:49
 0:22:51
0:22:51
 0:45:04
0:45:04
 0:03:58
0:03:58
 0:00:50
0:00:50
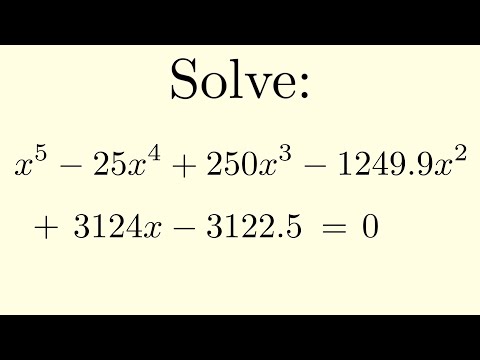 0:08:44
0:08:44
 0:45:24
0:45:24
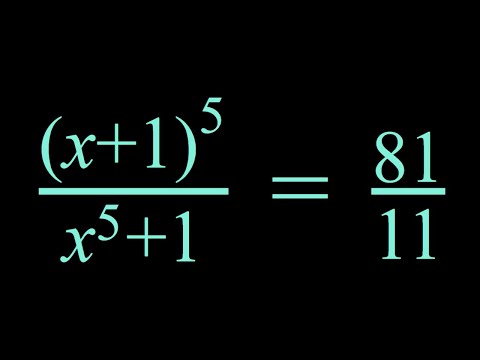 0:14:01
0:14:01
 0:00:26
0:00:26
 0:20:29
0:20:29
 0:29:02
0:29:02
 0:13:18
0:13:18
 0:00:37
0:00:37
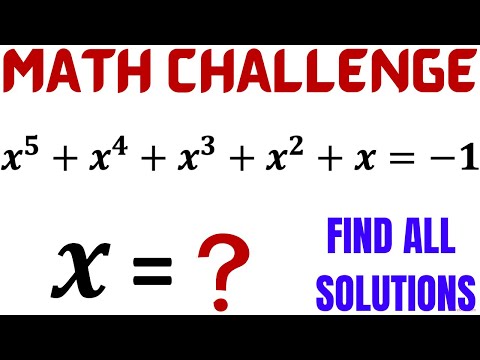 0:08:01
0:08:01
 0:06:38
0:06:38
 0:02:37
0:02:37
 0:10:33
0:10:33
 0:11:59
0:11:59
 0:04:17
0:04:17
 0:31:27
0:31:27
 0:00:58
0:00:58
 0:04:24
0:04:24
 0:00:25
0:00:25
 0:10:44
0:10:44