filmov
tv
Solving the Quintic Equation z^5 + 32 = 0 - Complex Analysis
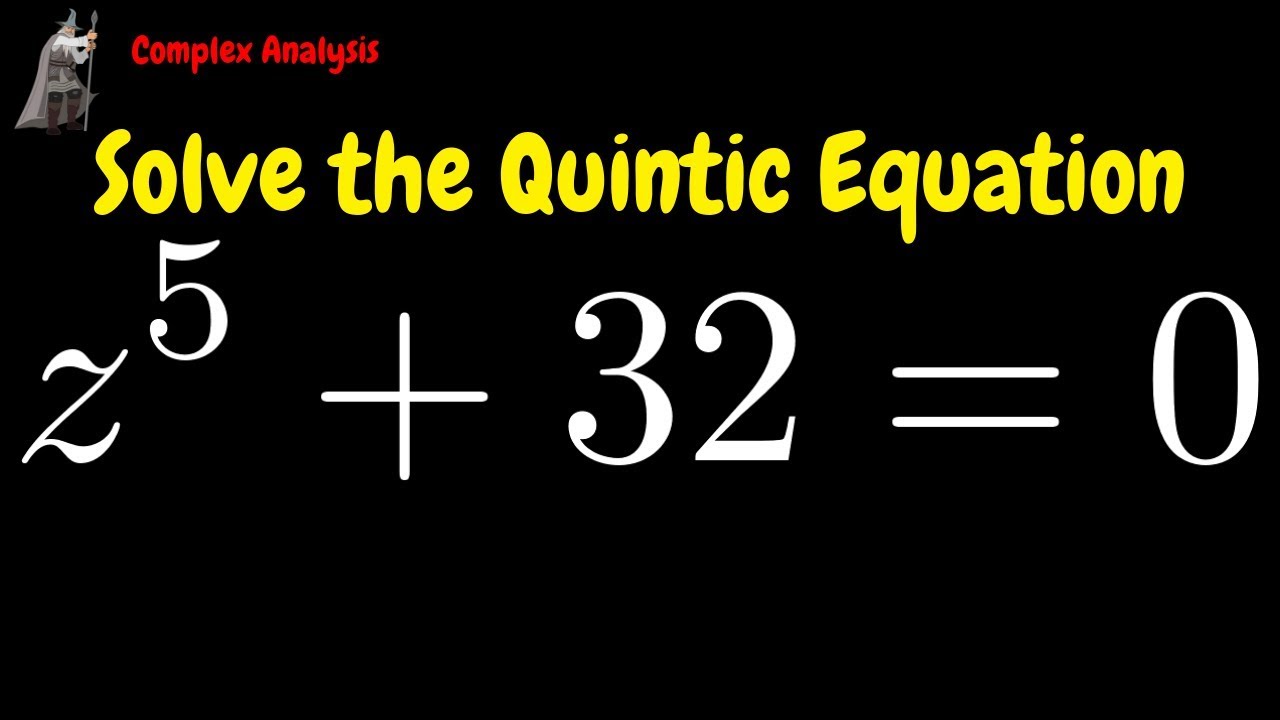
Показать описание
Solving the Quintic Equation z^5 + 32 = 0 - Complex Analysis
Solving the Quintic Equation z^5 + 32 = 0 - Complex Analysis
Find Complex Roots of a Cubic Equation z^3 - 3z^2 + z + 5 = 0
EXTREME quintic equation! (very tiring)
Why There's 'No' Quintic Formula (proof without Galois theory)
Complex Roots (5 of 5: Flowing Example - Solving z^6=64)
solving equations but they get increasingly awesome
5 simple unsolvable equations
When mathematicians get bored (ep1)
Solving A Quintic Equation without Using the Quintic Formula
Can You Solve a Quintic with Complex Roots? No? Then Watch!
I can solve any quintic equation!!
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
How REAL Men Integrate Functions
An Overview of the True Quintic Formula...and Why You Should Never Use It
My First Quintic Equation
A Nice Factorable Quintic | Problem 215
z^5+32=0
Find the roots of a fifth-degree polynomial (quintic)
de Moivre quintic formula
Can We solve A Quintic | Problem #126
Quintic Equation Mastery | Solutions by Complex Numbers
How To Solve A Quintic Equation | Algebra | Math Olympiad
How to Solve the Difficult Quintic Equation x^5+x^4+1=0?
Learn how to solve Quintic Equation (x^5)-(x^4)-(x^2)-=(5x^3)+6x quickly | Math Olympiad Training
Комментарии
 0:04:17
0:04:17
 0:05:54
0:05:54
 0:31:27
0:31:27
 0:45:04
0:45:04
 0:10:28
0:10:28
 0:10:44
0:10:44
 0:00:50
0:00:50
 0:00:37
0:00:37
 0:10:33
0:10:33
 0:07:19
0:07:19
 0:22:51
0:22:51
 0:00:38
0:00:38
 0:00:35
0:00:35
 0:35:21
0:35:21
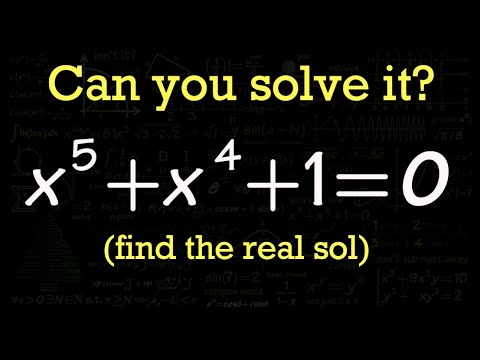 0:10:29
0:10:29
 0:09:33
0:09:33
 0:06:23
0:06:23
 0:07:20
0:07:20
 0:29:02
0:29:02
 0:12:40
0:12:40
 0:13:18
0:13:18
 0:10:42
0:10:42
 0:03:59
0:03:59
 0:07:13
0:07:13