filmov
tv
Real Analysis | The continuous image of a compact set.

Показать описание
We look at some topological implications of continuity. In particular, we prove that the continuous image of a compact set of real numbers is compact and use this to prove the extreme value theorem.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
Real Analysis 27 | Continuity and Examples
Real Analysis Live - Problem Solving - Continuous Functions
Real Analysis | Intro to uniform continuity.
Proof: f(x) = |x| is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Real Analysis 29 | Combination of Continuous Functions
Real Analysis | Showing a function is (dis)continuous.
Real Analysis 28 | Epsilon-Delta Definition
Real Analysis: Continuous Functions
Differentiability in Real Analysis | CSIR NET | IIT JAM | GATE | Lec- 40 | VedPrep Maths Academy
Composition of Continuous Functions is Continuous | Real Analysis
Proof: f(x) = x is Continuous using Epsilon Delta Definition | Real Analysis Exercises
What is Uniform Continuity?
Real Analysis 33 | Some Continuous Functions
Proof: e^x is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Real Analysis 30 | Continuous Images of Compact Sets are Compact
Real Analysis | The uniform continuity of sqrt(x).
When the continuous functions fails to be Onto | Real Analysis | Mathematics
Proof: sqrt(x) is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Real Analysis 40 | Local Extreme and Rolle's Theorem
Real Analysis: Continuous Functions
Real Analysis 23 | Sequence of Functions
Real Analysis | Showing a function is not uniformly continuous.
B.a|B.sc| Real Analysis |Riemann Integral |Integrability of Continuous function |CBLU|MDU|GJU|KUK|
Real Analysis I: L11 - Theory of continuous functions: a definition, some examples
Комментарии
 0:09:59
0:09:59
 2:13:26
2:13:26
 0:14:17
0:14:17
 0:04:19
0:04:19
 0:07:56
0:07:56
 0:12:41
0:12:41
 0:08:59
0:08:59
 0:06:01
0:06:01
 1:07:15
1:07:15
 0:04:53
0:04:53
 0:04:46
0:04:46
 0:06:23
0:06:23
 0:09:20
0:09:20
 0:14:36
0:14:36
 0:07:04
0:07:04
 0:14:17
0:14:17
 0:11:42
0:11:42
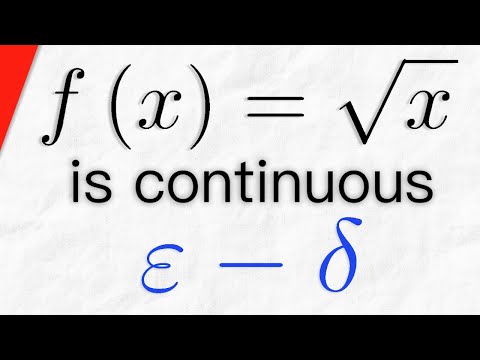 0:09:22
0:09:22
 0:11:39
0:11:39
 0:12:07
0:12:07
 0:06:27
0:06:27
 0:18:36
0:18:36
 0:14:48
0:14:48
 0:47:52
0:47:52