Real Analysis | Showing a function is (dis)continuous.

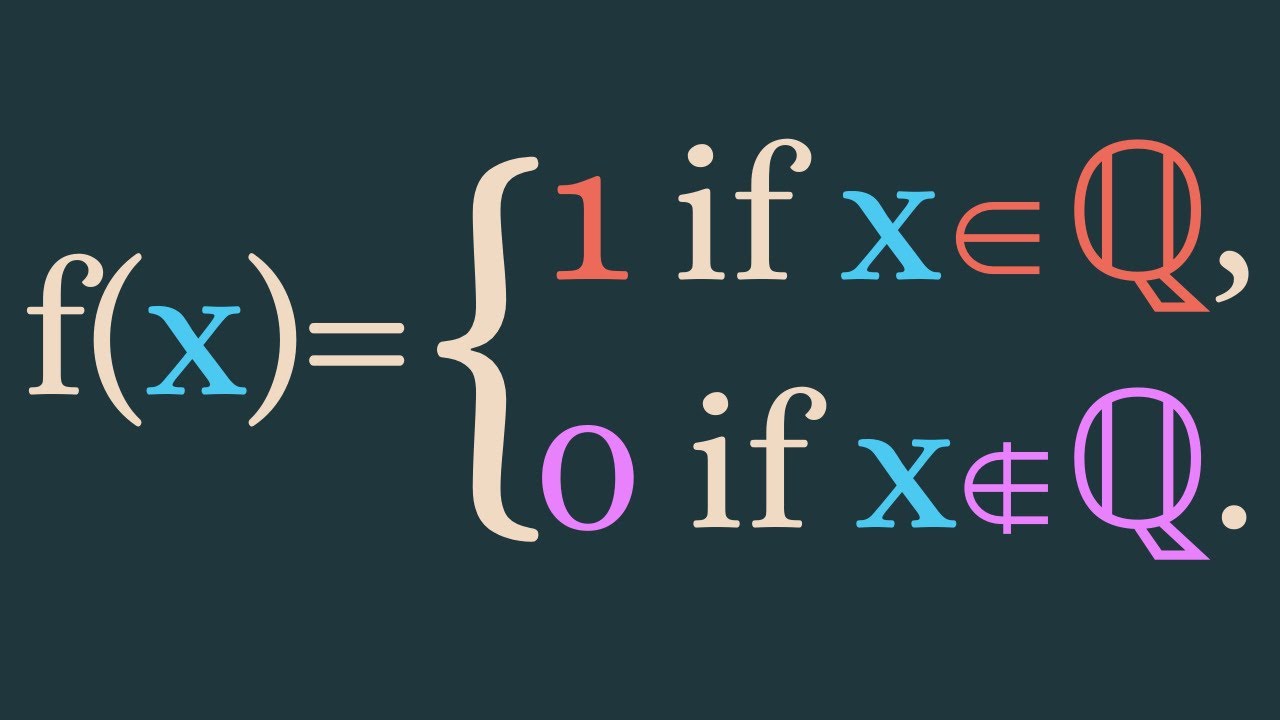
Показать описание

We give an example of showing a function is continuous everywhere and present a classic example of a function that is nowhere continuous.

If you are going to use an ad-blocker, considering using brave and tipping me BAT!

Books I like:

Abstract Algebra:

Differential Forms:

Number Theory:

Analysis:

Calculus:

My Filming Equipment:

Рекомендации по теме

Комментарии

There is actually another way of proving continuity of x^2, i.e. that the limit of x^2 = a^2 as x goes to a.
|x^2 - a^2| = |x - a| * |x + a| = |x - a| * |x - a + 2a| <= |x - a| * ( |x-a| + 2|a| ). So it suffices to make the extreme right less than epsilon.

This way you don't have to worry about bounding |x+a|, you only have |x-a| to work with.

backyard

12:38

12:00 “Because 0 is not equal to 1” Proof ? 😛

goodplacetostop

My Calculus Professor (Tony Tromba, UC Santa Cruz 1981) dropped the Dirichlet Function on us at the end of a Friday lecture to give something to discuss at Happy Hour.

douglasstrother

This was amazingly accessible, thank you. Could you do a video explaining constructive logic and how to prove there? How to rationalize sequential continuity without L.E.M

SimplyChrisRLP

Thanks a lot for this marvelous video!!! The second example was the one what I was looking for

sadececansu

Baby Penn be like : *High pitched sound*

ArthurDetaille

in the first example you can take delta to be -a+sqrt(a^2+e) and than you have (x-a)(x+a) is less than a^2+e-a^2=e.

yoav

I've found very interesting and brilliant equation that I can't solve. The command for the task: Solve cos(cos(cos(cos(x)))) = sin(sin(sin(sin(x)))). x is a real number. This problem comes from Russian Math Olympiad, 95. Michael, I believe you can overcome this task :)

xutzl

Very cool, thanks for the quality in all the aspects!!!

JorgeGomez-litd

when i saw the function that u gonna present in the video i was genuinely amazed

xaxuser

Here is a nice related problem: it can be shown that function f(x)=0, x is irrational, 1/n if x=m/n, gcd(m, n)=1 is continuous in all irrational points and not continuous in all rational. The question therefore is: is there a reverse function, not continuous in all irrational points and continuous in all rational?

sirlight-ljij