filmov
tv
Real Analysis 29 | Combination of Continuous Functions
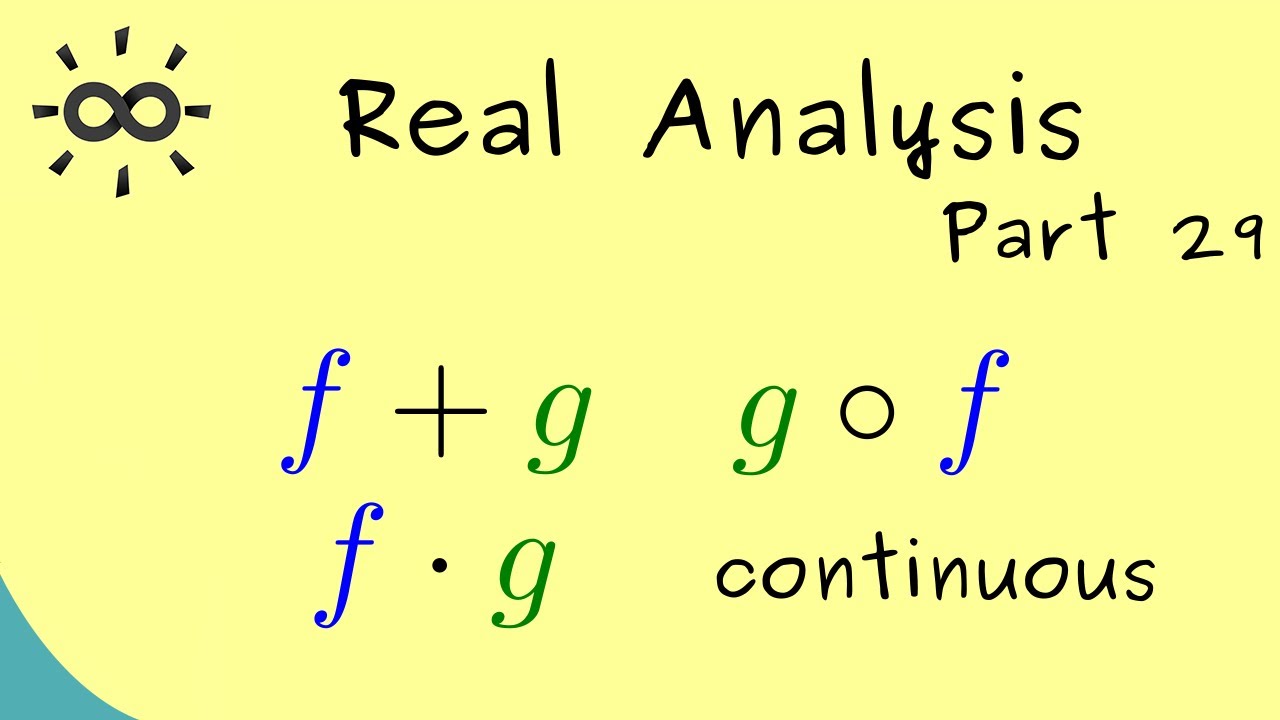
Показать описание
Please consider to support me if this video was helpful such that I can continue to produce them :)
🙏 Thanks to all supporters! They are mentioned in the credits of the video :)
This is my video series about Real Analysis. We talk about sequences, series, continuous functions, differentiable functions, and integral. I hope that it will help everyone who wants to learn about it.
x
00:00 Intro
00:14 Recalling continuity
01:25 Combining 2 continuous functions
03:07 Composition of functions
05:55 Proof for composition of functions
07:27 Credits
#RealAnalysis
#Mathematics
#Calculus
#LearnMath
#Integrals
#Derivatives
I hope that this helps students, pupils and others. Have fun!
(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
Real Analysis 29 | Combination of Continuous Functions
Real Analysis 29 | Combination of Continuous Functions [dark version]
Combinations of continuous functions
Real Analysis 27 | Continuity and Examples
Most💯 Important Step Before any Procedure 🔥
Intro. to Real Analysis: Lecture 18.2 - Limits of Combinations of Functions
mat 311, Real Analysis,5.2 Combination of Continuous Functions L2
Real Analysis Live - Problem Solving - Continuous Functions
ZEN COIN DAILY COMBO TODAY
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Intro Real Analysis, Lec 29: The Most Beautiful Equation in the World, Taylor Series Calculations
Real Analysis 28 | Epsilon-Delta Definition
Real Analysis 33 | Some Continuous Functions
Real Analysis 30 | Continuous Images of Compact Sets are Compact
UPSC VS IIT JEE 🥵 #iitstatus #motivation #toppers #iitjee #jeemains #upscstatus #neet #nit #jee
Undergraduate Real Analysis Topic List | Herndon Math Services
Real Analysis by Bartle || Section#5.2 Combination of Continuous Functions with theorem and examples
Aspirants practicing eatingetiquette # SSB #SSBPreparation #NDA #CDS #Defence #DefenceAcademy
That trainer who only focuses on girls | trainers be like
Real Analysis 36 | Chain Rule
Logical Reasoning???#viral #vidumzn
QUESTION 29 CSIR NET DEC 2015 REAL ANALYSIS FIXED POINT THEOREM CONTINUOUS IIT JAM SOLUTION
Real Analysis 28 | Epsilon-Delta Definition [dark version]
power of ifs officer 🔥| isiliye kahte ias ips ifa bano 🔥🔥🔥 | watch it for really hard motivation |...
Комментарии
 0:07:56
0:07:56
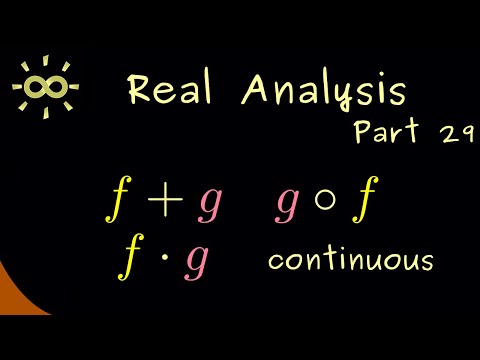 0:07:43
0:07:43
 0:13:02
0:13:02
 0:09:59
0:09:59
 0:00:16
0:00:16
 0:22:27
0:22:27
 0:12:54
0:12:54
 2:13:26
2:13:26
 0:44:04
0:44:04
 0:00:16
0:00:16
 0:55:40
0:55:40
 0:08:59
0:08:59
 0:09:20
0:09:20
 0:07:04
0:07:04
 0:00:14
0:00:14
 0:50:57
0:50:57
 0:19:41
0:19:41
 0:00:11
0:00:11
 0:01:01
0:01:01
 0:06:17
0:06:17
 0:00:11
0:00:11
 0:01:38
0:01:38
 0:08:46
0:08:46
 0:00:42
0:00:42