filmov
tv
Real Analysis 10 | Bolzano-Weierstrass Theorem

Показать описание
Please consider to support me if this video was helpful such that I can continue to produce them :)
🙏 Thanks to all supporters! They are mentioned in the credits of the video :)
This is my video series about Real Analysis. We talk about sequences, series, continuous functions, differentiable functions, and integral. I hope that it will help everyone who wants to learn about it.
x
00:00 Intro
00:20 Bolzano-Weierstrass theorem
01:13 Proof
05:42 Credits
#RealAnalysis
#Mathematics
#Calculus
#LearnMath
#Integrals
#Derivatives
I hope that this helps students, pupils and others. Have fun!
(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
Real Analysis 10 | Bolzano-Weierstrass Theorem
Real Analysis 10 | Bolzano-Weierstrass Theorem [dark version]
The Bolzano–Weierstrass theorem, a proof from real analysis
Short Proof of Bolzano-Weierstrass Theorem for Sequences | Real Analysis
The Bolzano Weierstrass Theorem
A Better Bolzano-Weierstrass Proof
Proving Bolzano-Weierstrass with Nested Interval Property | Real Analysis
An application of the Bolzano-Weierstrass theorem | Real Analysis
Bolzano Weierstrass rap -- Visualized
Intro Real Analysis, Lec 8: Subsequences, Bolzano-Weierstrass, Cauchy Criterion, Limsup & Liminf
#10 Real Analysis | Bolzano-Weierstrass Theorem | Hunter College
Real Analysis, Lecture 11 (Bolzano–Weierstrass theorem and Cauchy=Convergent for sequences)
The Bolzano Weierstraß Theorem
Intro. to Real Analysis: Lecture 14.2 - The Bolzano Weierstrass Proof using Peaks
BOLZANO WEIERSTRASS THEOREM || Bolzano Weierstrass theory || SEQUENCE ||sequence
The Bolzano-Weierstrass Theorem in ℝ — Intuition in Real Analysis Part 1
Lecture 10, Real Analysis, Week of 2/15-2/19 - Bolzano-Weierstrass & the Cauchy Criterion
Bolzano-Weierstrass Theorem [Real Analysis]
Real Analysis: Bolzano Weierstrass Theorem | Unit-2 | CC-3
🔶09 - Bound Set and Bolzano Weierstrass Theorem | Upper Bounds, Lower Bounds and Limit Points
The Bolzano-Weierstrass Theorem
Real Analysis | Bolzano Weierstrass Theorem | Proof
Subsequence and Bolzano Weierstrass Theorem|Real Analysis Lecture 20|BSc/BS/MSc Mathematics Lectures
Bolzano weierstrass theorem l real Analysis l BWT l
Комментарии
 0:06:12
0:06:12
 0:05:58
0:05:58
 0:13:30
0:13:30
 0:05:21
0:05:21
 0:07:44
0:07:44
 0:06:14
0:06:14
 0:16:18
0:16:18
 0:07:12
0:07:12
 0:04:00
0:04:00
 0:57:23
0:57:23
 0:12:07
0:12:07
 0:46:12
0:46:12
 0:05:48
0:05:48
 0:28:49
0:28:49
 0:00:13
0:00:13
 0:22:15
0:22:15
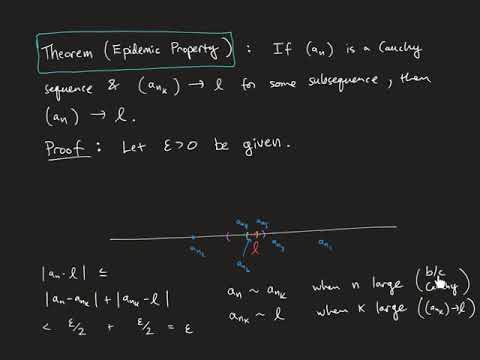 0:53:41
0:53:41
 0:06:32
0:06:32
 0:00:35
0:00:35
 0:23:39
0:23:39
 1:00:56
1:00:56
 0:07:26
0:07:26
 0:13:41
0:13:41
 0:07:41
0:07:41