filmov
tv
6/2(1+2) or 6÷2(1+2) equals ? The truth.

Показать описание
Also check this out:
My previous video on the subject:
Music by Bertrand Laurence
used with permission.
Find me on FaceBook:
My previous video on the subject:
Music by Bertrand Laurence
used with permission.
Find me on FaceBook:
6÷2(1+2) = ? Correct Answer Explained By Mathematician
Math Prof answers 6÷2(1+2) = ? once and for all ***Viral Math Problem***
6/2(1+2) or 6÷2(1+2) equals ? The truth.
PEMDAS is wrong
The Problem with PEMDAS: Why Calculators Disagree
6÷2(1+2) = ? Correct Answer Explained | Viral Math Problem | Viral Math Problem 6÷2(1+2)=
Viral Math Problem 6➗2(1+ 2)= ? Correct Answer Explained by mathematician!
6÷2(1+2)=? correctly explained.
Sudoku Arrow Party Balloons
What is 6÷2(1+2) = ? Viral Math Videos
6/2(1+2)= SOLVED. WITH PROOF!! (Watch until end)
6÷2(1+2) = ? | Correct Answer Inside Finally Solved!! | PEMDAS/BIDMAS is Wrong?!
POLÊMICA: 6/2(1+2) ou 6÷2(1+2) é igual a 1 ou 9? MANEIRA CORRETA DE RESOLVER!
9 TIMES TABLE #shorts #math #maths #mathematics
1 2 3 4 5 6 7 8 9 0 | Number Lore
Meet the Math Facts Addition & Subtraction - 2+4=6
Сколько будет 6/2(1+2)
Learning Math
Approximating 2+2
1 2 3 4 5 6 7 8 9 10
Why is pi here? And why is it squared? A geometric answer to the Basel problem
1 2 Buckle My Shoes - EXTRA CURSED #shorts
Butterfly Method for Subtracting Fractions 📚 #Shorts #math #maths #mathematics #education #learn
Multiples of 8 😎 #Shorts #math #maths #mathematics
Комментарии
 0:05:33
0:05:33
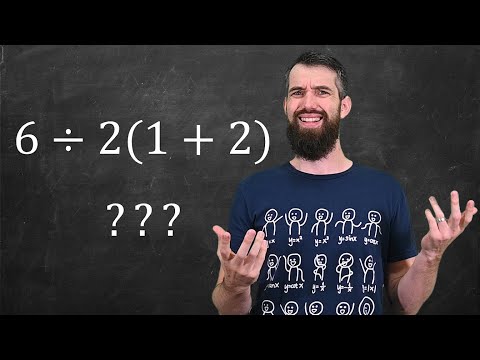 0:06:04
0:06:04
 0:10:20
0:10:20
 0:08:12
0:08:12
 0:17:27
0:17:27
 0:00:42
0:00:42
 0:06:18
0:06:18
 0:08:16
0:08:16
 0:25:10
0:25:10
 0:03:36
0:03:36
 0:02:34
0:02:34
 0:11:14
0:11:14
 0:04:20
0:04:20
 0:00:23
0:00:23
 0:00:37
0:00:37
 0:02:13
0:02:13
 0:00:59
0:00:59
 0:02:37
0:02:37
 0:00:40
0:00:40
 0:00:26
0:00:26
 0:17:08
0:17:08
 0:00:18
0:00:18
 0:00:15
0:00:15
 0:00:20
0:00:20