filmov
tv
6/2(1+2)= SOLVED. WITH PROOF!! (Watch until end)

Показать описание
How to solve for 6/2(1+2)= with explanation.
I am Asian.
I am Asian.
6/2(1+2)= SOLVED. WITH PROOF!! (Watch until end)
6÷2(1+2) = ? Correct Answer Explained By Mathematician
6/2 (1+2) had the world stumped but we finally have an answer! #shorts #maths #mathstricks
Math Prof answers 6÷2(1+2) = ? once and for all ***Viral Math Problem***
6÷2(1+2)=???
6÷2(1+2) answer with proof.
PEMDAS is wrong
6 : 2 ( 1 + 2 ) Viral Math Problem #shorts
6 ÷ 2(1+2) = ?
6:2 (1+2) = POPRAWNE ROZWIĄZANIE ZADANIA - MaturaToBzdura.TV
6/2(1+2) or 6÷2(1+2) equals ? The explanation!
6 ÷ 2(1+2) = ?
Human Calculator Solves World’s Longest Math Problem #shorts
6÷2(1+2) = ?
6÷2(1+2) = ? Correct Answer Explained | Viral Math Problem | Viral Math Problem 6÷2(1+2)=
Japanese Method #shorts #fyp
Facebook's Trickiest Viral Math Problem Explained! [6/2(1+2)]
India vs japan || mathematics challenge || 😅🤣🤣🤭
6÷2(1+2) = ? | Correct Answer Inside Finally Solved!! | PEMDAS/BIDMAS is Wrong?!
6÷2(1+2) = ? | Correct Answer Inside Finally Solved!!
6 ÷ 2 (2 + 1) = CORRECT WAY TO SOLVE
5 simple unsolvable equations
6÷2(1+2) = ? Mathematician Explains The Correct Answer | Viral Twitter Problem Solved By Aman Sir
6:2(1+2)= Viral Math Problem Explained By Mathematician
Комментарии
 0:02:34
0:02:34
 0:05:33
0:05:33
 0:00:50
0:00:50
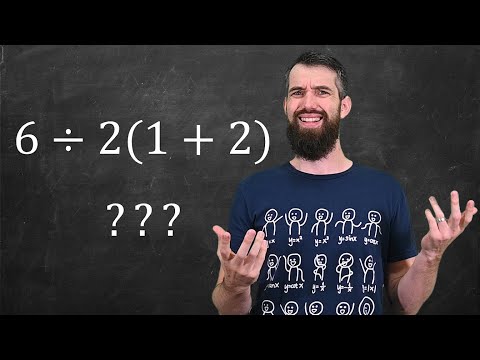 0:06:04
0:06:04
 0:01:21
0:01:21
 0:07:23
0:07:23
 0:08:12
0:08:12
 0:00:22
0:00:22
 0:01:00
0:01:00
 0:03:13
0:03:13
 0:03:35
0:03:35
 0:00:15
0:00:15
 0:00:34
0:00:34
 0:00:17
0:00:17
 0:00:42
0:00:42
 0:00:20
0:00:20
 0:05:01
0:05:01
 0:00:12
0:00:12
 0:11:14
0:11:14
 0:08:31
0:08:31
 0:03:44
0:03:44
 0:00:50
0:00:50
 0:09:02
0:09:02
 0:04:34
0:04:34