filmov
tv
Math Prof answers 6÷2(1+2) = ? once and for all ***Viral Math Problem***

Показать описание
lol, am I really doing this? Ok, fine. There is a ***viral math problem*** about, uh, order of operations. You know, #BEDMAS or #PEMDAS. The most common form is 6/2(1+2) but it also shows up as 60/5(7-5) and other equivalent forms. What is the correct answer explained by a math prof? Sorry, I don't care. But I'm happy to share a few thoughts on why I think this issue repeatedly going viral says some things about societal views of mathematics.
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
Math Prof answers 6÷2(1+2) = ? once and for all ***Viral Math Problem***
6÷2(1+2)=???
6/2 (1+2) had the world stumped but we finally have an answer! #shorts #maths #mathstricks
Viral Math Problem 6➗2(1+ 2)= ? Correct Answer Explained by mathematician!
6 : 2 ( 1 + 2 ) Viral Math Problem #shorts
6 ÷ 2(1+2) = ?
6÷2(1+2) = ? Correct Answer Explained | Viral Math Problem | Viral Math Problem 6÷2(1+2)=
Viral math Problem 6 ÷ 2 (1+2 ) = ? correct answer explain by mathematician
Solving Quadratic Equations by Factoring | Finding the Roots | Part 1 |
6÷2(1+2) = ? Mathematician Explains The Correct Answer | Viral Twitter Problem Solved By Aman Sir
PEMDAS is wrong
What is 6÷2(1+2) = ? The Correct Answer Explained
6÷2(1+2) = ? | Correct Answer Inside Finally Solved!! | PEMDAS/BIDMAS is Wrong?!
6/2(1+2) = ? CORRECT ANSWER
6÷2(1+2) = ?
Viral Math Problem 6➗2(1+ 2)= ? Correct Answer Explained by mathematician!
3+6 divided by 2 = 6??
India vs japan || mathematics challenge || 😅🤣🤣🤭
Rätsel - Mathe | Welcher Taschenrechner hat recht? - 6:2(1+2) | Mathe einfach erklärt!
Table of 5 #mathsscam #tables #shorts #5
Human Calculator Solves World’s Longest Math Problem #shorts
Indian vs Japanese Maths 🔥| Vedic Maths Trick for Fast Calculation | Speed Maths #trending #shorts...
6÷2(1+2)=? correctly explained.
PEMDAS Math Problem | Algebra Fundamentals | JusticeTheTutor #math #shorts #maths #mathstricks
Комментарии
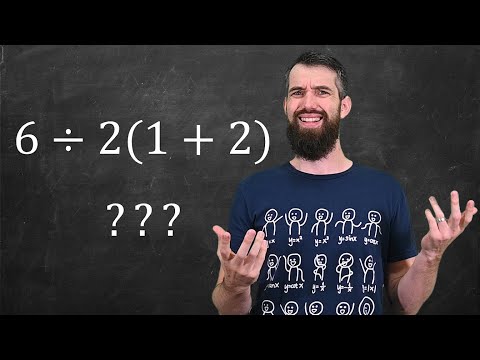 0:06:04
0:06:04
 0:01:21
0:01:21
 0:00:50
0:00:50
 0:06:18
0:06:18
 0:00:22
0:00:22
 0:01:00
0:01:00
 0:00:42
0:00:42
 0:03:32
0:03:32
 0:27:16
0:27:16
 0:09:02
0:09:02
 0:08:12
0:08:12
 0:04:00
0:04:00
 0:11:14
0:11:14
 0:03:41
0:03:41
 0:00:17
0:00:17
 0:02:23
0:02:23
 0:00:10
0:00:10
 0:00:12
0:00:12
 0:04:36
0:04:36
 0:00:23
0:00:23
 0:00:34
0:00:34
 0:00:13
0:00:13
 0:08:16
0:08:16
 0:00:29
0:00:29