filmov
tv
Why is pi here? And why is it squared? A geometric answer to the Basel problem
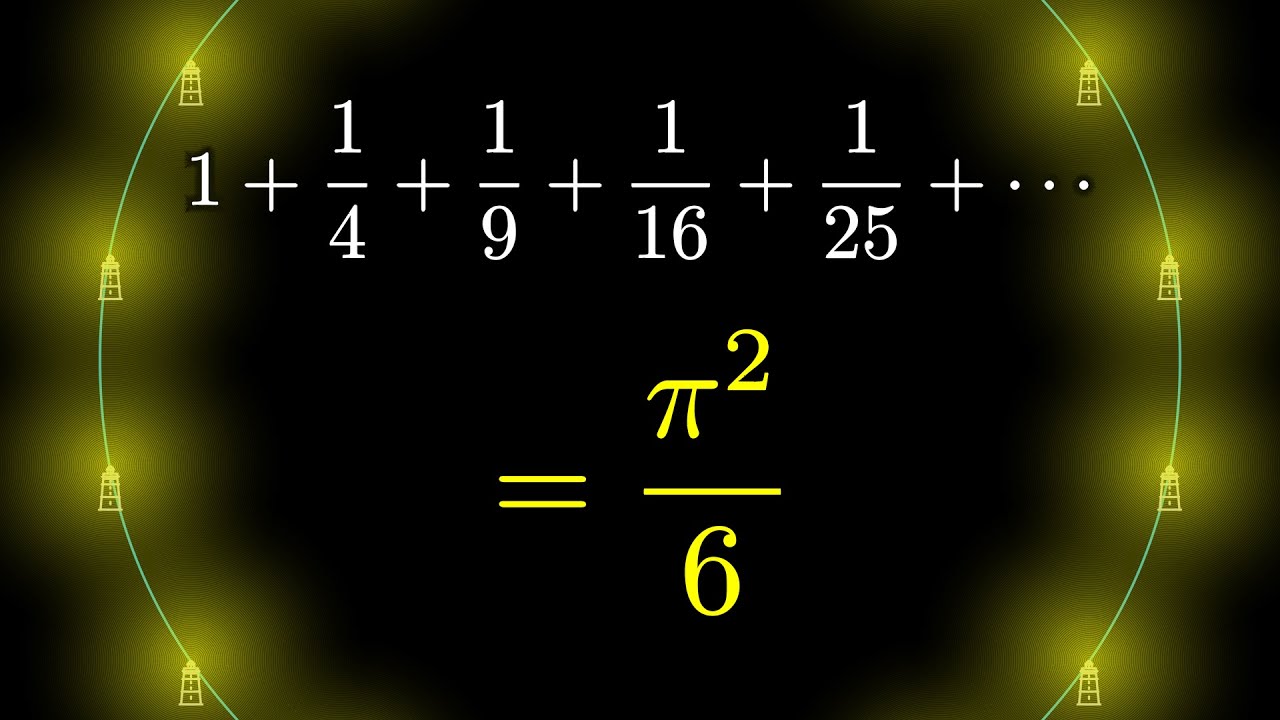
Показать описание
A most beautiful proof of the Basel problem, using light.
An equally valuable form of support is to simply share some of the videos.
Brilliant's principles list that I referenced:
Get early access and more through Patreon:
The content here was based on a paper by Johan Wästlund
Check out Mathologer's video on the many cousins of the Pythagorean theorem:
On the topic of Mathologer, he also has a nice video about the Basel problem:
A simple Geogebra to play around with the Inverse Pythagorean Theorem argument shown here.
Some of you may be concerned about the final step here where we said the circle approaches a line. What about all the lighthouses on the far end? Well, a more careful calculation will show that the contributions from those lights become more negligible. In fact, the contributions from almost all lights become negligible. For the ambitious among you, see this paper for full details.
If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.
Music by Vincent Rubinetti:
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
------------------
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).
Various social media stuffs:
An equally valuable form of support is to simply share some of the videos.
Brilliant's principles list that I referenced:
Get early access and more through Patreon:
The content here was based on a paper by Johan Wästlund
Check out Mathologer's video on the many cousins of the Pythagorean theorem:
On the topic of Mathologer, he also has a nice video about the Basel problem:
A simple Geogebra to play around with the Inverse Pythagorean Theorem argument shown here.
Some of you may be concerned about the final step here where we said the circle approaches a line. What about all the lighthouses on the far end? Well, a more careful calculation will show that the contributions from those lights become more negligible. In fact, the contributions from almost all lights become negligible. For the ambitious among you, see this paper for full details.
If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.
Music by Vincent Rubinetti:
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
------------------
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).
Various social media stuffs:
Комментарии
 0:17:08
0:17:08
 0:10:30
0:10:30
 0:05:45
0:05:45
 0:14:29
0:14:29
 0:15:16
0:15:16
 0:24:46
0:24:46
 0:11:03
0:11:03
 0:01:29
0:01:29
 0:05:53
0:05:53
 0:30:42
0:30:42
 0:00:31
0:00:31
 0:15:51
0:15:51
 0:00:11
0:00:11
 0:14:01
0:14:01
 0:01:15
0:01:15
 0:01:00
0:01:00
 0:08:33
0:08:33
 0:07:58
0:07:58
 0:15:21
0:15:21
 0:04:49
0:04:49
 0:00:41
0:00:41
 0:09:01
0:09:01
 0:08:24
0:08:24
 0:26:38
0:26:38