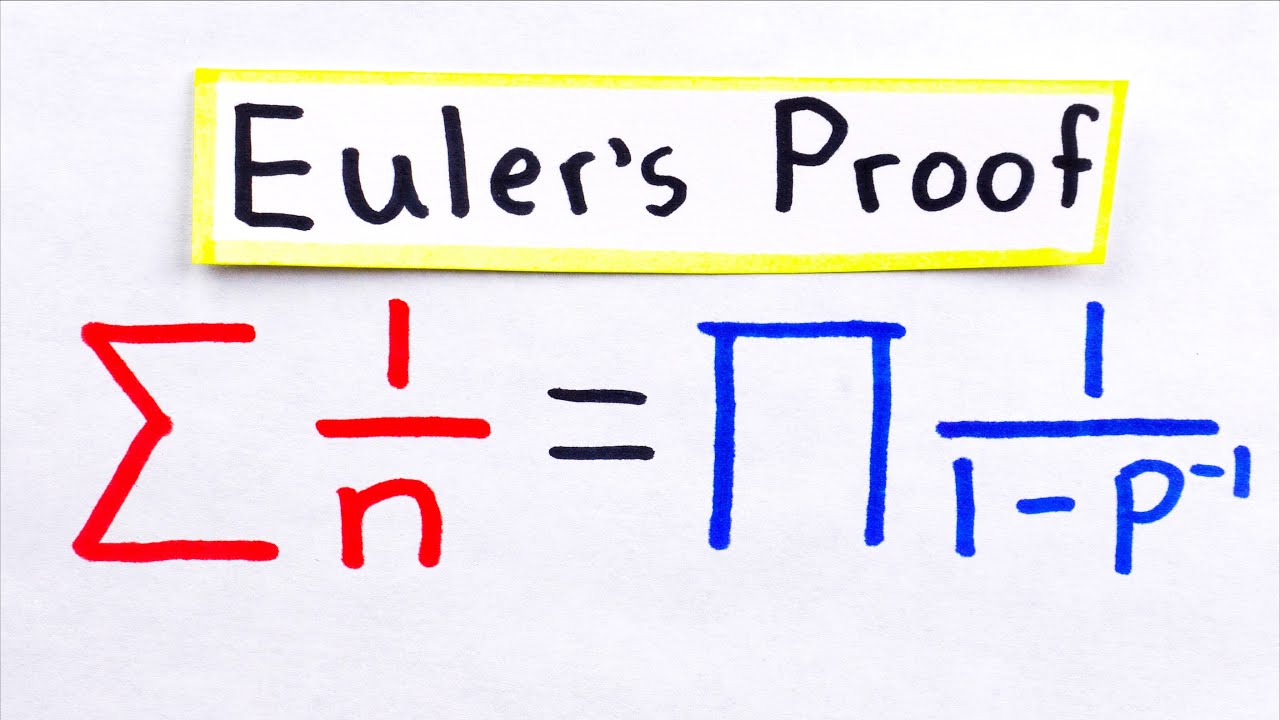
Euler's Proof of the Infinitude of Primes

Around 300 BC Euclid proved the infinitude of primes using a simple argument typically presented as a contradiction proof. In the 1700s the singularly prolific mathematician Leonhard Euler proved the infinitude of primes essentially as a corollary of a deeper result concerning the equality of the Riemann Zeta function with a product of prime-related factors. In this video we go over Euler's classic proof of this ancient result. #maths #primenumber #mathematics

Join Wrath of Math to get exclusive videos, lecture notes, and more:

Textbooks I Like!

★DONATE★

Follow Wrath of Math on...

0:00 Intro
1:40 Setting the Stage
4:06 Start Proof
7:41 Identifying Pattern
9:53 Key Division Step
10:55 When s=1
13:00 Harmonic Series
16:22 The Final Step

[WrathofMath]

CORRECTION: 12:46 is a logical error. The convergence of the sum on the left does not imply finitely many primes, because it is certainly possible the product on the right consists of infinitely many factors yet still converges. Only that remark was incorrect, the logic of the actual argument made in the video is correct. It is the case that finitely many primes would imply convergence of the product, which thus implies convergence of the sum. Hence if the sum diverges it must be that the product diverges, which is only possible if there are infinitely many primes.

[hugh]

This is such a chaotic channel. Infinite products over the primes one week, short division the next...

[RobertShadowLee]

8:50 The proof strongly relies on the Fundamental Theorem of Arithmetic, and one might ask whether the infinitude of primes is required to prove the FTA, as this could make the proof circular. However, it turns out that you can prove the FTA without assuming the infinitude of primes, so it all works out. Still, it would be helpful to clarify this, as brief details like this can nullify the validity of a proof.

[MH-sfjz]

The way of reasoning does not work by arguing for s>1, because it is never established the product is continuous in s.

[ronhoffman]

Really liked the method for deriving the equality. Very interesting.

[Iponamann]

I found this proof unsatisfactory because of how you let s=1. The equality of the infinite sum and product was proved assuming that s is strictly greater than 1. It would be enough to show that the function Sum(1 to infinity) 1/n^s is unbounded for s in (1, infinity), but this was not done. If someone can provide me a proof of this please let me know.

[k.chriscaldwell]

Which introduces a paradox in that the products of primes grows faster than the primes and so crowds out future primes. A graph of the primes illustrates this.

[AsiccAP]

This feels non-rigorous to me.The proof the equality for s>1 seems sound to me, but why can we assert that it also works with s=1? The entire principal of the proof for s>1 is multiplying infinite series and subtracting them, which doesnt make sense if they diverge in the first place. Even the "equality" of s=1 case doesn't make sense, since the Left hand side diverges to infinity, you basically are saying something "equals infinity", which doesn't make sense in the real number system, as infinity is not a real number.

[markwrede]

Multiplication delivers a vast cycle of integers, eventually failing to distinguish values. These are distinguished not by primes, but by the sequential differences between primes. Phi describes this slope value for all twin primes: 5, 7, 13, 19, 31, 43, .... Other such values exist as well, with the same properties for the square primes (square root of 11 divided by 4), sexy primes (square root of 29 divided by 6), and so on.

[MacHooolahan]

The most astounding result in maths - nice vid....

[crazyape]

Strangely, "sieve" is pronounced "siv", not "seev". 8:25 Great proof, BTW. I can't believe how simple it was.

[CreativeGuy]

It's a really well explained video, but I have a doubt Ithink that there's an error, at
6:20 the factctor of the sum should only be 1/3^s and not (1/3^s) * (1 - 1/2^s)

[psymar]

This is kind of neat, but it still feels less intuitive than the much older proof that there are infinitely many primes:
Suppose there are finitely many primes. Then you can make a list of all of them. Multiply all the primes in your list and add one. Call this number N. If you divide N by any prime in your list, you'll have a remainder of 1, so it's not divisible by any of them. But either it's prime, or it's divisible by at least one prime not in your list -- so anytime you have a list of "all primes" you actually don't, there's always another prime.

[atrus]

This would have been a lot clearer if you wrote the product as 1/(1 - 1/p^s). You could then right away see the relationship to the seemingly arbitrary multiplying you were doing. In fact, why not start with the equality and multiply on both sides.

[jaimeduncan]

The sum on the right diverges, it makes no sense to say it’s equal to any value. I will say the argument is fun but in pretty shaky foundation.

[rockapedra]

11:03 wait ... At this point we still don't know the multiplication is infinite, right?

[ilmiohandle]

Does somebody resemble some similarity with Eratosthenes sieve in the derivation of the infinte product? I found it amazing!Great video!

[hdthor]

Seems much easier to just do a proof by contradiction. Suppose there were a finite set of primes P, then the number that is (the product of the elements of P) + 1 is therefore is congruent to 1 modulo p for each p in P. Because it’s never congruent to 0 modulo any prime, it is not a composite, and so it is a prime, and therefore is an element of P. But it is bigger than any element in P. Contradiction. So P must be infinite.

[OfficialStickPM]

What purpose would anything under 3 and over 5 would ever be needed to understand? Can you explain that to me in another video or a reply so I can grasp why you want all these ?

[_tech]

If s = 2 then it we have primpes products on right