filmov
tv
ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = -1/12
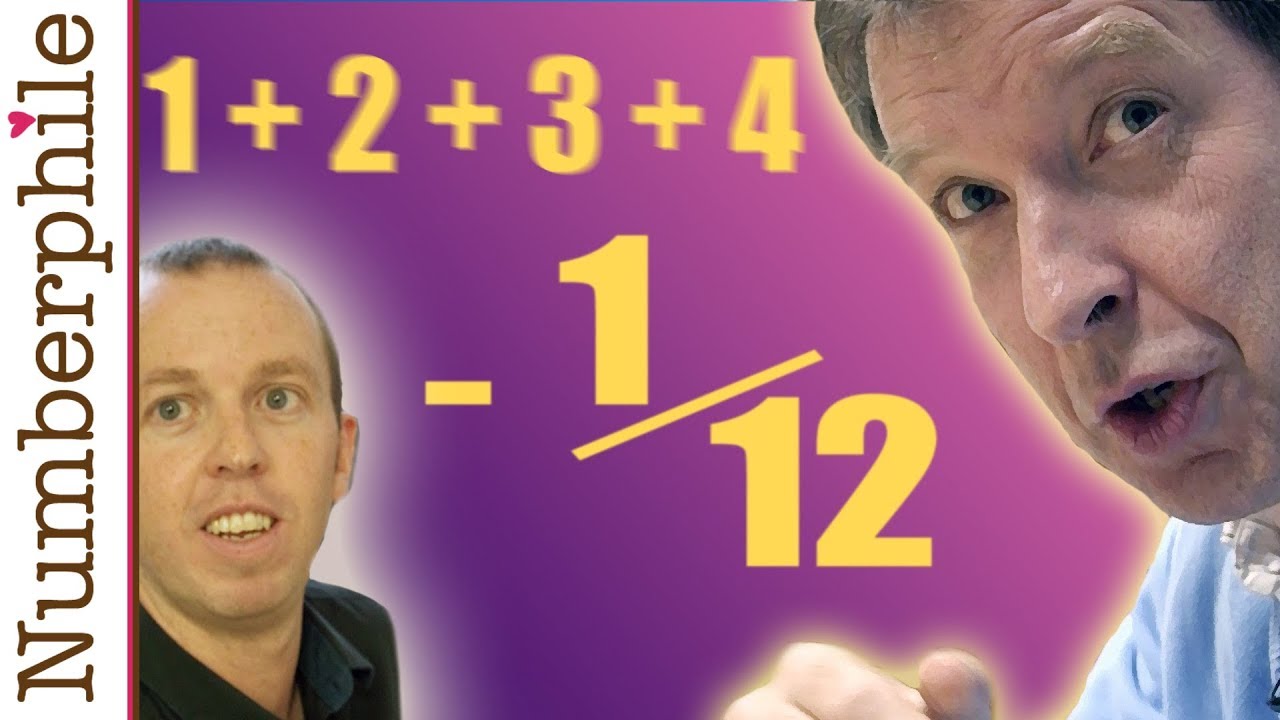
Показать описание
More links & stuff in full description below ↓↓↓
The sum of all natural numbers (from 1 to infinity) produces an "astounding" result.
Tony Padilla and Ed Copeland are physicists at the University of Nottingham.
We also hear that Chapter XIII of Konrad Knopp's book, "Theory and Application of Infinite Sequences and Series", is very good if you can get your hands on it.
NUMBERPHILE
Videos by Brady Haran
The sum of all natural numbers (from 1 to infinity) produces an "astounding" result.
Tony Padilla and Ed Copeland are physicists at the University of Nottingham.
We also hear that Chapter XIII of Konrad Knopp's book, "Theory and Application of Infinite Sequences and Series", is very good if you can get your hands on it.
NUMBERPHILE
Videos by Brady Haran
ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = -1/12
math for fun, I am spiderman vs. the astounding 1+2+3+...=?
Yakima’s Mahre brothers reflect on their astounding 1-2 Olympic finish 38 years later
Hidden 𝜋 - An Astounding Integral [ ln^2(x)/(x^2+1) from 0 to 1 ]
The Queen's Gambit. -- Beth plays white. 'You're astounding'
Ramanujan's astounding invention.(1+2+3+......)=-1/12
The Most Astounding Fact - Neil deGrasse Tyson
The Astounding Conversion of Paul (Acts 9:1–9)
Counting by 100 to 1000 song | Learn to count by 100 till 1000 | Epic Giant Kids Songs
Honest Carpets Introduces Astounding 1 and 2
Half-Life 2: Astounding AI
🔥Astounding 🤯 Ramanujan👍 Summation 😃Maths fun#maths #mathsmagic #funmaths #astounding #ramanujan...
Astounding New Evidence of the Two Witnesses
🤯Ramanujan Summation🔥 Astounding😯 #maths #ramanujan #mathsmagic #mathstricks #funfacts #funmaths...
1 Kings 12-22 (Part 2) | The Astounding Power of Unfailing Faith
Bookworm Adventures Volume 2 - BOOK 6 (ASTOUNDING PLANET): Chapter 1 - Space Traveling
That's astounding
Things under microscope 😱#shorts#subscribe #facts #creepy #amazing #astounding
Grandi Series|Ramanujan Summation|Astounding|Maths|Fun maths|PD TUTORIAL
Rent this astounding 1 Bedroom Flat in London SE17 1GF | RentLondonFlat.com
Psalm 91:1-2 | what an astounding assurance 2024
Astounding Stories Vol. One Part 1 - The Beetle Horde Chapters 1-2
Rent this astounding 1 Bedroom Flat in Whitechapel London E1 8AS | RentLondonFlat.com
A quick Portal 2 video, presenting an astounding 1080p 60fps standard.
Комментарии
 0:07:50
0:07:50
 0:06:08
0:06:08
 0:24:26
0:24:26
 0:11:16
0:11:16
 0:01:45
0:01:45
 0:16:34
0:16:34
 0:03:34
0:03:34
 0:52:52
0:52:52
 0:01:53
0:01:53
 0:01:08
0:01:08
 0:00:49
0:00:49
 0:00:58
0:00:58
 0:44:02
0:44:02
 0:01:00
0:01:00
 0:12:28
0:12:28
 0:03:19
0:03:19
 0:00:06
0:00:06
 0:00:17
0:00:17
 0:01:22
0:01:22
 0:03:05
0:03:05
 0:00:51
0:00:51
 0:38:21
0:38:21
 0:02:06
0:02:06
 0:00:32
0:00:32