filmov
tv
Can a continuous function from 2D to 3D be onto?

Показать описание
Are you ready to dive into the world of topology and analysis? Today, we explore an intriguing question: Can a continuous function from 2D to 3D be onto?
We take a deep dive into the concept of space-filling curves and the relationship between continuity and dimensionality. You'll learn about the limits and possibilities of continuous functions and discover the beauty and complexity of the mathematical world. This video is perfect for students looking to expand their understanding of mathematical concepts and deepen their appreciation for the subject. Get ready to be excited by the endless possibilities of math, and join us on this journey of discovery!
Music creds:
Home-Prod. Riddiman
We take a deep dive into the concept of space-filling curves and the relationship between continuity and dimensionality. You'll learn about the limits and possibilities of continuous functions and discover the beauty and complexity of the mathematical world. This video is perfect for students looking to expand their understanding of mathematical concepts and deepen their appreciation for the subject. Get ready to be excited by the endless possibilities of math, and join us on this journey of discovery!
Music creds:
Home-Prod. Riddiman
3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus
Can A Function Be Continuous At Only One Point?
Limit of a Function l What is a Continuous Function?
What is a continuous function?
Defining a function at a point to make it continuous | Limits | Differential Calculus | Khan Academy
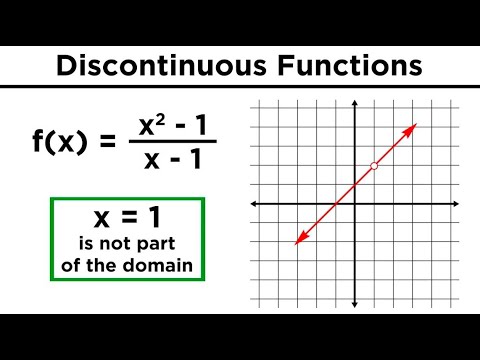
Continuous, Discontinuous, and Piecewise Functions
Continuity and Differentiability EXPLAINED with Examples
Is the function continuous or not
25. Cumulative Distribution Function for Continuous Random variable #probabilitydistribution
Is the function continuous?
Calculus - Continuous functions
Continuous and Uniformly Continuous Functions
Continuity and Differentiability
Real Analysis 27 | Continuity and Examples
Find the Value of a so that the Function is Continuous Everywhere
Find the value k that makes the function continuous
How many continuous functions are there ?
Continuous Function | Continuity of a Function 1
How to determine if a function is continuous and differentiable
Real Analysis 29 | Combination of Continuous Functions
Is a Function Discrete or Continuous?
Find the values a and b that make the piecewise function continuous
Determine the discontinuity of the function
Real Analysis: Continuous Functions
Комментарии
 0:10:10
0:10:10
 0:14:21
0:14:21
 0:07:23
0:07:23
 0:15:27
0:15:27
 0:04:57
0:04:57
 0:05:18
0:05:18
 0:05:33
0:05:33
 0:00:54
0:00:54
 0:11:39
0:11:39
 0:12:42
0:12:42
 0:08:45
0:08:45
 0:05:13
0:05:13
 0:32:48
0:32:48
 0:09:59
0:09:59
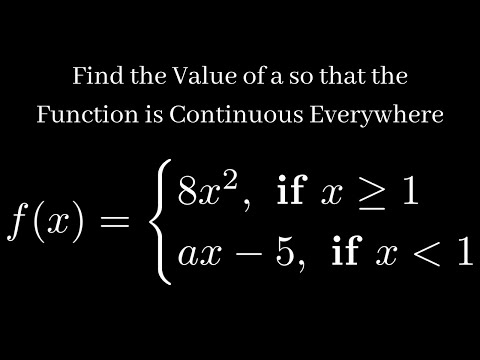 0:03:09
0:03:09
 0:02:50
0:02:50
 0:12:53
0:12:53
 0:08:38
0:08:38
 0:02:21
0:02:21
 0:07:56
0:07:56
 0:03:57
0:03:57
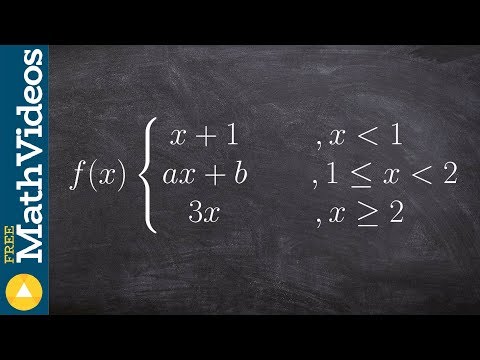 0:03:44
0:03:44
 0:01:05
0:01:05
 0:06:01
0:06:01