filmov
tv
Can A Function Be Continuous At Only One Point?

Показать описание
We find a function which is continuous at a single point, and discontinuous everywhere else. The first half of the video covers intuition for continuity, plus its formal definition.
00:00 Intuition
02:00 Refined intuition
04:08 Formal definition
06:39 Constructing an example
08:15 Proving continuity
10:22 Proving discontinuity
12:28 Further examples
00:00 Intuition
02:00 Refined intuition
04:08 Formal definition
06:39 Constructing an example
08:15 Proving continuity
10:22 Proving discontinuity
12:28 Further examples
Can A Function Be Continuous At Only One Point?
Defining a function at a point to make it continuous | Limits | Differential Calculus | Khan Academy
Is the function continuous or not
Is the function continuous?
Calculus - Continuous functions
Find the values a and b that make the piecewise function continuous
How to determine if a function is continuous and differentiable
Find the Value of a so that the Function is Continuous Everywhere
25. Cumulative Distribution Function for Continuous Random variable #probabilitydistribution
Continuous, Discontinuous, and Piecewise Functions
Find the value k that makes the function continuous
II PUC:When is a Function said to be Continuous|Dr.Rajkumar's Learning App|Reach Further|Mathem...
Limit of a Function l What is a Continuous Function?
The EASY way to find if a function is continuous #shorts (#continuity formula) is it continuous?
Determine if the Piecewise Function is Continuous by using the Definition of Continuity
Find the value k that makes the piecewise function continuous
Continuous Function | Continuity of a Function 1
Determine if the Function is Continuous from the Graph and Explain
Find a and b if f(x) is continuous everywhere
Show that f(x) is continuous at x=4
Example: When is a Piecewise Function Continuous?
Determine if a piecewise function is continuous or discontinuous
How to find the value k that makes the function continuous
Combining Continuous Functions
Комментарии
 0:14:21
0:14:21
 0:04:57
0:04:57
 0:00:54
0:00:54
 0:12:42
0:12:42
 0:08:45
0:08:45
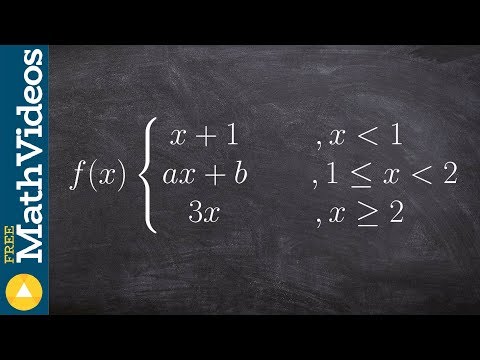 0:03:44
0:03:44
 0:02:21
0:02:21
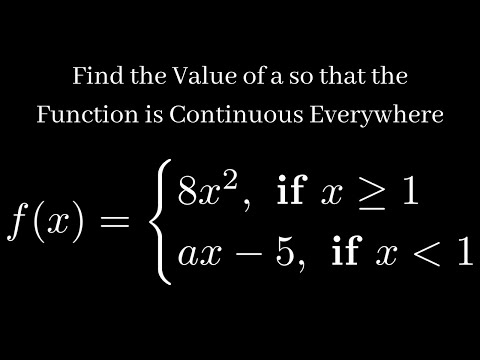 0:03:09
0:03:09
 0:11:39
0:11:39
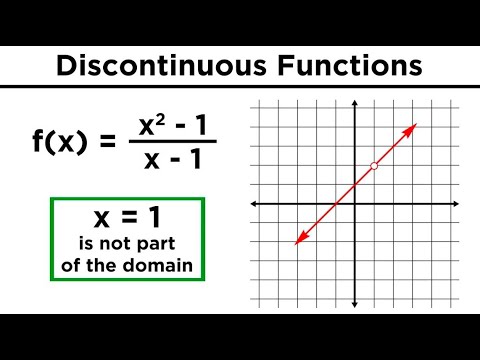 0:05:18
0:05:18
 0:02:50
0:02:50
 0:03:56
0:03:56
 0:07:23
0:07:23
 0:00:37
0:00:37
 0:04:01
0:04:01
 0:02:03
0:02:03
 0:08:38
0:08:38
 0:03:51
0:03:51
 0:10:36
0:10:36
 0:01:51
0:01:51
 0:03:18
0:03:18
 0:01:45
0:01:45
 0:01:54
0:01:54
 0:08:25
0:08:25